Zufallsvariable (Thema: Stochastik)

Schnellübersicht

1. Einführung in Zufallsvariablen

Eine Zufallsvariable ist eine Funktion. Sie weist den möglichen Elementarereignissen eines Zufallsexperiments bestimmte Werte zu. Beispielsweise lässt es sich mit den Elementarereignissen eines Münzwurfs (Wappen, Zahl) nicht allzu gut rechnen, daher werden diese über eine Zufallsvariable zu 0 und 1 „umgewandelt”. Die Funktion der Zufallsvariablen wird gewöhnlich mit „X” bezeichnet. Nachfolgend einmal die Unterschiede zur vermutlich eher bekannten Schreibweise von Funktionen, nämlich f(x)=y:
Das kleine w (X(ω)) ist tatsächlich ein kleines Omega. Es wird verwendet, da die Zufallsvariable jedes Elementarereignis aus dem Ergebnisraum (Ω, großes Omega) auf einen neuen Wert (x) abbildet.

2. Beispiel Münzwurf

Bereits zuvor wurde der Münzwurf erwähnt. Der Ergebnisraum des Münzwurfs ist Ω={Wappen, Zahl}. Die Elementarereignisse sind daher ω1=Wappen und ω2=Zahl. Eine passende Zufallsvariable könnte nun Wappen auf „0” und Zahl auf „1” abbilden. Die etwas komplizierte Schreibweise dafür lautet nun:

3. Beispiel Würfelwurf

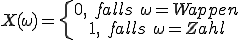
Ähnlich zum Münzwurf können wir auch eine Zufallsvariable für den Würfelwurf aufstellen. Diese ist etwas umfangreicher, da der Ergebnisraum mehr mögliche Elementarereignisse enthält (Ω={Augenzahl 1, Augenzahl 2, Augenzahl 3, Augenzahl 4, Augenzahl 5, Augenzahl 6}). Die Zufallsvariable könnte wie folgt lauten:
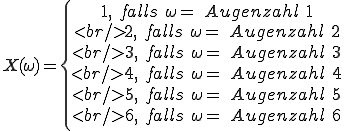Würde man bei der Definition der möglichen Elementarereignisse direkt die Augenzahl (1, 2, 3, ...) verwenden (statt „Augenzahl 1”, „Augenzahl 2”, ...), dann könnte man sich die umfangreiche Definition der Zufallsvariablen auch sparen und schlicht schreiben: X(ω)=ω.
Aber auch andere Zufallsvariablen können für den Würfelwurf definiert werden. Zum Beispiel könnten wir allen geraden Zahlen eine 1 und allen ungeraden Zahlen eine 0 zuweisen:

4. Diskrete und stetige Zufallsvariablen

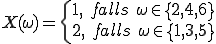
Bisher haben wir (zur Vereinfachung) immer vorausgesetzt, dass jedes Zufallsexperiment eine endliche Anzahl von Elementarereignissen haben kann. So hat z. B. der Münzwurf zwei Elementarereignisse oder der Würfelwurf sechs. Auch wenn wir 100.000 verschiedene Würfel gleichzeitig werfen, würden wir noch immer eine endliche Anzahl verschiedener Elementarereignisse erhalten (6100.000). Es gibt aber auch Zufallsexperimente, die theoretisch unendlich viele verschiedene Elementarereignisse erzeugen können.

Beispiel: Angenommen wir wollen ein derartiges Experiment bilden. Wir bauen dazu eine Wurfmaschine auf, die Katzen zwischen 10 und 15m weit schleudert. Wie weit genau sie innerhalb dieses Bereichs fliegen entscheidet der Zufall. Nach dem Aufprall messen wir die Flugweite mit unendlicher Genauigkeit. Dementsprechend können die Katzen im Bereich zwischen 10 und 15m an unendlich vielen Punkten aufschlagen, denn die Weite lässt sich beliebig unterteilen (z. B. 10,0 oder 10,01 oder 10,00001 oder 10,000000000001 usw.).

Bildet man die Elementarereignisse des Zufallsexperiments nun über eine Zufallsvariable ab, dann wird diese Funktion als stetig bezeichnet. Merkmal jeder stetigen Zufallsvariable ist, dass sie zumindest in einem Intervall jeden Wert aus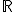 oder aus einem Teilbereich von 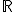annehmen kann (und 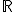enthält unendlich viele Werte). Würde man diese Funktion in einem Graph eintragen, dann hätte diese — zumindest in einem Teilbereich — keine „Lücken”, daher der Begriff „stetig”.

Das Gegenteil einer stetigen Funktion ist die diskrete Funktion. Diese ergibt häufig Werte aus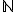 , z. B. 1, 2, 3, ... Die zuvor genannten Zufallsvariablen für den Würfel- und den Münzwurf waren diskret (Münzwurf: die Funktion nimmt nur zwei verschiedene Werte an, Würfelwurf (1): sechs verschiedene Werte, Würfelwurf (2): zwei verschiedene Werte). Die genaue Definition lautet, dass eine Funktion dann als diskret bezeichnet wird, wenn sie nur endlich oder abzählbar unendlich viele Werte annehmen kann. Der Begriff „abzählbar unendlich” ist etwas schwieriger zu verstehen. Vereinfacht ausgedrückt heißt es, dass eine Funktion dann abzählbar unendlich viele Werte annimmt, wenn man die Werte in jedem Teilbereich der nicht bis unendlich reicht zählen könnte. Nimmt etwa eine Funktion in einem Teilbereich alle Werte aus 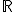an, dann ist sie nicht abzählbar unendlich, denn die Werte von 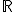lassen sich beliebig unterteilen, sodass man sie nicht durchzählen kann. Nimmt aber eine Funktion alle Werte aus 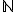an, dann ergibt sie zwar unendlich viele Werte, ist aber dennoch abzählbar unendlich, denn die Werte aus jedem Teilbereich können gezählt werden (auch wenn das mitunter recht lange dauern kann).

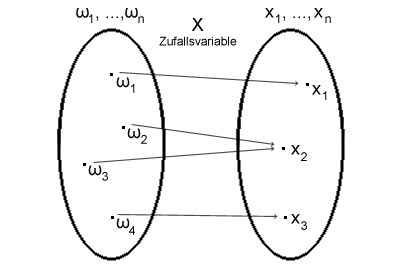
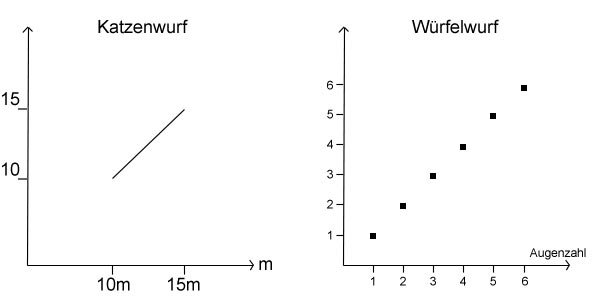
Die unten stehende Abbildung zeigt eine stetige Zufallsvariable (Katzenwurf) und eine diskrete Zufallsvariable (Würfelwurf: Augenzahl).

5. Quiz

6. Links

• Zusammenfassung zu Zufallsvariable, Wahrscheinlichkeitsverteilung und mehr
• Wikipedia zur Zufallsvariable (englisch)