Schnellübersicht
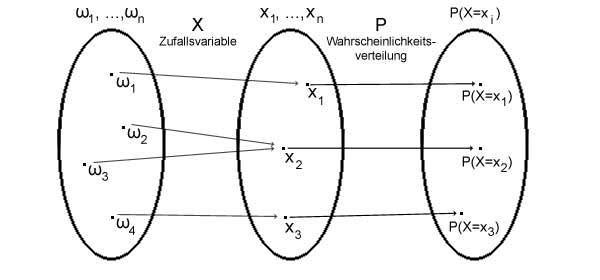
Eine Wahrscheinlichkeitsverteilung hat Ähnlichkeit mit einer Zufallsvariablen. Es ist ebenfalls eine Funktion. Sie ordnet den Werten der Zufallsvariablen Wahrscheinlichkeiten zu. Von den Elementarereignissen aus bis zu den Wahrscheinlichkeiten ist der Weg also in etwa der nachfolgenden Abbildung zu entnehmen:
Für die Wahrscheinlichkeit des Wertes xi aus einer Zufallsvariablen X wird geschrieben: P(X = xi) = p, wobei p eine Wahrscheinlichkeit ist. Häufig werden die Wahrscheinlichkeiten den Werten der Zufallsvariablen anhand einer Tabelle zugeordnet, welche in etwa folgendes Aussehen haben kann:
Gehen wird nun beispielhaft von einem Münzwurf aus. Dieser kann die Elementarereignisse ω1=Wappen und ω1=Zahl haben. Über die Zufallsvariable X wird dem Elementarereignis „Wappen” eine 0 und dem Elementarereignis „Zahl” eine 1 zugeordnet:
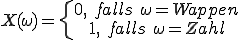 Wir definieren nun die Wahrscheinlichkeitsverteilung, die den Werten von X über eine Tabelle ihre Wahrscheinlichkeiten zuordnet:
Wir definieren nun die Wahrscheinlichkeitsverteilung, die den Werten von X über eine Tabelle ihre Wahrscheinlichkeiten zuordnet:
Es gilt also für den Wert xi=0 (entspricht Wappen): P(X = 0) = 0,5 bzw. 50% Wahrscheinlichkeit. Analog gilt für xi=1 (entspricht Zahl) ebenfalls: P(X = 1) = 0,5 bzw. 50% Wahrscheinlichkeit.
Das vorherige Beispiel war ein wenig einfach, daher nehmen wir nun den gleichzeitigen Wurf von zwei Würfeln. Die Elementarereignisse können z. B. lauten (1, 1), (4, 5), (6, 1), (6, 6) usw. Jedem dieser Würfelpaare ordnen wir nun über eine Zufallsvariable seine Augensumme zu:
Jetzt können wir diesen Werten der Zufallsvariablen über eine Wahrscheinlichkeitsverteilung ihre Wahrscheinlichkeiten zuordnen. Die Augensummen gehen von 2 bis 12. Es gibt insgesamt 36 verschiedene Zahlenpaare. Die Häufigkeit jeder einzelnen Augensumme kann abgezählt werden. Es ergibt sich folgende Tabelle:
Die Werte aus dem Beispiel zum doppelten Würfelwurf können nun weiterverwendet werden, um die Wahrscheinlichkeiten verschiedener Ereignisse zu bestimmen. Jeder Wert der Wahrscheinlichkeitsverteilung gibt die Wahrscheinlichkeit eines bestimmten Elementarereignisses wider. Durch Addition und Subtraktion lassen sich die Elementarereignisse nun miteinander verknüpfen.
Beispiel 1: Definieren wir das Ereignis E: „Augensumme größer als 6”. Die Wahrscheinlichkeit dieses Ereignisses ist:
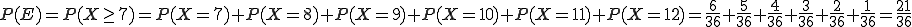
Beispiel 2: Definieren wir das Ereignis E: „Augensumme zwischen 5 und 8, aber nicht 7”. Dies berechnet sich wie folgt:
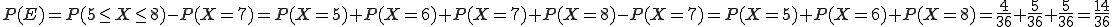
Ein Histogramm ist ein Diagramm, dass die Wahrscheinlichkeiten in einem Koordinatensystem darstellt. Dazu werden die Werte aus der Zufallsvariablen (x1, x2, ..., xn) auf der x-Achse eingetragen und die möglichen Wahrscheinlichkeiten auf der y-Achse. Anhand von Balken wird die Zuordnung der Wahrscheinlichkeiten zu den Werten aus der Zufallsvariable dargestellt. Die Höhe der Balken entspricht jeweils deren Wahrscheinlichkeit (bei einer Wahrscheinlichkeit von 0,5 würde der Balken also bei einer Höhe von 0,5 enden). Von der Breite her bedeckt jeder Balken einen kompletten x-Wert. Würde also etwa gelten P(xi=2)=0,5 und der nächste definierte Wert xi=3 sein, dann würde der Balken den Bereich zwischen 2 und 3 bedecken.
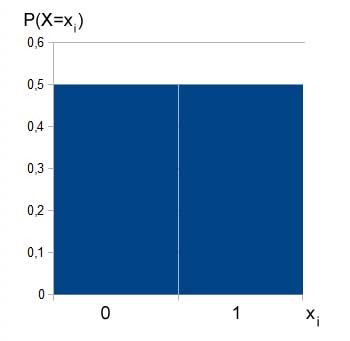
Beispiel 1: Das Histogramm für das erste Beispiel (Münzwurf) sieht wie folgt aus:
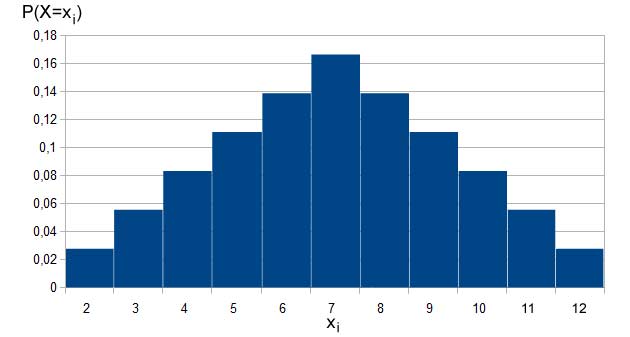
Beispiel 2: Das Histogramm für den Münzwurf ist nicht sonderlich spektakulär. Das für den doppelten Würfelwurf sieht schon etwas interessanter aus:
Gut zu sehen ist, dass die Augensumme „in der Mitte” (7) die höchste Wahrscheinlichkeit hat, während die Extreme am Rand eher selten vorkommen.
Die kumulative Verteilungsfunktion (Schreibweise: F(x)) verwendet die Werte aus der Wahrscheinlichkeitsverteilung und kumuliert diese, sie werden also aufaddiert. Jeder Wert F(x) entspricht daher P(X ≤ x). Für das Beispiel mit dem doppelten Würfelwurf würde das folgende Tabelle ergeben:
Der Wert von F(x) für x=1 entspricht also P(X=1). Der für x=2 entspricht P(X=1)+P(X=2). Der für x=3 entspricht P(X=1)+P(X=2)+P(X=3) usw. Das heißt auch, dass F(x) immer dem Wert von P(X≤x) entspricht. Wird daher verlangt, den Wert von P(X ≤ 5) zu bestimmen, dann kann einfach der Wert F(5) verwendet werden, sofern die kumulative Verteilungsfunktion zur Verfügung steht.
An der letzten definierten Stelle muss die kumulative Verteilungsfunktion immer den Wert 1 haben, da sie an dieser Stelle sämtliche Wahrscheinlichkeiten der Wahrscheinlichkeitsverteilung summiert (und diese müssen die Wahrscheinlichkeit 1 bzw. 100% haben).
- Die Wahrscheinlichkeitsverteilung verwendet die Werte einer Zufallsvariable und ordnet diesen Wahrscheinlichkeiten zu. Schreibweise: P(X = xi) = y. Heißt: Wert x der Zufallsvariable X hat Wahrscheinlichkeit y.
- Die Zuordnung von Wahrscheinlichkeit y zu Wert xi erfolgt häufig über eine Tabelle.
- Die kumulative Verteilungsfunktion (Schreibweise: F(x)) kumuliert die Werte xi≤x von P(X), sodass gilt F(x) = P(X ≤ x).
1. Einleitung zur Wahrscheinlichkeitsverteilung
Eine Wahrscheinlichkeitsverteilung hat Ähnlichkeit mit einer Zufallsvariablen. Es ist ebenfalls eine Funktion. Sie ordnet den Werten der Zufallsvariablen Wahrscheinlichkeiten zu. Von den Elementarereignissen aus bis zu den Wahrscheinlichkeiten ist der Weg also in etwa der nachfolgenden Abbildung zu entnehmen:
Für die Wahrscheinlichkeit des Wertes xi aus einer Zufallsvariablen X wird geschrieben: P(X = xi) = p, wobei p eine Wahrscheinlichkeit ist. Häufig werden die Wahrscheinlichkeiten den Werten der Zufallsvariablen anhand einer Tabelle zugeordnet, welche in etwa folgendes Aussehen haben kann:
| xi | 1 | 2 | 3 | 4 | 5 |
| P(X = xi) | 0,10 | 0,25 | 0,17 | 0,13 | 0,35 |
2. Beispiel Münzwurf
Gehen wird nun beispielhaft von einem Münzwurf aus. Dieser kann die Elementarereignisse ω1=Wappen und ω1=Zahl haben. Über die Zufallsvariable X wird dem Elementarereignis „Wappen” eine 0 und dem Elementarereignis „Zahl” eine 1 zugeordnet:
| xi | 0 | 1 |
| P(X = xi) | 0,50 | 0,50 |
3. Doppelter Würfelwurf
Das vorherige Beispiel war ein wenig einfach, daher nehmen wir nun den gleichzeitigen Wurf von zwei Würfeln. Die Elementarereignisse können z. B. lauten (1, 1), (4, 5), (6, 1), (6, 6) usw. Jedem dieser Würfelpaare ordnen wir nun über eine Zufallsvariable seine Augensumme zu:
| Elementarereignis | xi |
| (1, 1) | 2 |
| (1, 2) | 3 |
| (1, 3) | 4 |
| (1, 4) | 5 |
| (1, 5) | 6 |
| (1, 6) | 7 |
| (2, 1) | 3 |
| (2, 2) | 4 |
| (2, 3) | 5 |
| (2, 4) | 6 |
| (2, 5) | 7 |
| (2, 6) | 8 |
| (3, 1) | 4 |
| (3, 2) | 5 |
| (3, 3) | 6 |
| (3, 4) | 7 |
| (3, 5) | 8 |
| (3, 6) | 9 |
| (4, 1) | 5 |
| (4, 2) | 6 |
| (4, 3) | 7 |
| (4, 4) | 8 |
| (4, 5) | 9 |
| (4, 6) | 10 |
| (5, 1) | 6 |
| (5, 2) | 7 |
| (5, 3) | 8 |
| (5, 4) | 9 |
| (5, 5) | 10 |
| (5, 6) | 11 |
| (6, 1) | 7 |
| (6, 2) | 8 |
| (6, 3) | 9 |
| (6, 4) | 10 |
| (6, 5) | 11 |
| (6, 6) | 12 |
| xi | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| P(X = xi) |
4. Rechnen mit den Werten der Wahrscheinlichkeitsverteilung
Die Werte aus dem Beispiel zum doppelten Würfelwurf können nun weiterverwendet werden, um die Wahrscheinlichkeiten verschiedener Ereignisse zu bestimmen. Jeder Wert der Wahrscheinlichkeitsverteilung gibt die Wahrscheinlichkeit eines bestimmten Elementarereignisses wider. Durch Addition und Subtraktion lassen sich die Elementarereignisse nun miteinander verknüpfen.
Beispiel 1: Definieren wir das Ereignis E: „Augensumme größer als 6”. Die Wahrscheinlichkeit dieses Ereignisses ist:
Beispiel 2: Definieren wir das Ereignis E: „Augensumme zwischen 5 und 8, aber nicht 7”. Dies berechnet sich wie folgt:
5. Histogramm
Ein Histogramm ist ein Diagramm, dass die Wahrscheinlichkeiten in einem Koordinatensystem darstellt. Dazu werden die Werte aus der Zufallsvariablen (x1, x2, ..., xn) auf der x-Achse eingetragen und die möglichen Wahrscheinlichkeiten auf der y-Achse. Anhand von Balken wird die Zuordnung der Wahrscheinlichkeiten zu den Werten aus der Zufallsvariable dargestellt. Die Höhe der Balken entspricht jeweils deren Wahrscheinlichkeit (bei einer Wahrscheinlichkeit von 0,5 würde der Balken also bei einer Höhe von 0,5 enden). Von der Breite her bedeckt jeder Balken einen kompletten x-Wert. Würde also etwa gelten P(xi=2)=0,5 und der nächste definierte Wert xi=3 sein, dann würde der Balken den Bereich zwischen 2 und 3 bedecken.
Beispiel 1: Das Histogramm für das erste Beispiel (Münzwurf) sieht wie folgt aus:
Beispiel 2: Das Histogramm für den Münzwurf ist nicht sonderlich spektakulär. Das für den doppelten Würfelwurf sieht schon etwas interessanter aus:
Gut zu sehen ist, dass die Augensumme „in der Mitte” (7) die höchste Wahrscheinlichkeit hat, während die Extreme am Rand eher selten vorkommen.
6. Kumulative Verteilungsfunktion
Die kumulative Verteilungsfunktion (Schreibweise: F(x)) verwendet die Werte aus der Wahrscheinlichkeitsverteilung und kumuliert diese, sie werden also aufaddiert. Jeder Wert F(x) entspricht daher P(X ≤ x). Für das Beispiel mit dem doppelten Würfelwurf würde das folgende Tabelle ergeben:
| xi | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| F(x) |
Der Wert von F(x) für x=1 entspricht also P(X=1). Der für x=2 entspricht P(X=1)+P(X=2). Der für x=3 entspricht P(X=1)+P(X=2)+P(X=3) usw. Das heißt auch, dass F(x) immer dem Wert von P(X≤x) entspricht. Wird daher verlangt, den Wert von P(X ≤ 5) zu bestimmen, dann kann einfach der Wert F(5) verwendet werden, sofern die kumulative Verteilungsfunktion zur Verfügung steht.
An der letzten definierten Stelle muss die kumulative Verteilungsfunktion immer den Wert 1 haben, da sie an dieser Stelle sämtliche Wahrscheinlichkeiten der Wahrscheinlichkeitsverteilung summiert (und diese müssen die Wahrscheinlichkeit 1 bzw. 100% haben).