Schnellübersicht
Die Poissonverteilung wird in der Regel eingesetzt, um die Wahrscheinlichkeit von Ereignissen innerhalb eines bestimmten Zeitraums zu bestimmen. Beispielsweise könnte man ermitteln, wie wahrscheinlich es ist, dass innerhalb von 5 Minuten x Autos eine bestimmte Kreuzung passieren. Zur Berechnung der Poissonverteilung wird der Erwartungswert als Vorgabe benötigt. Statt E(X) hat es sich allerdings eingebürgert, diesen in der Formel mit λ zu repräsentieren. Die Berechnung erfolgt dann über:
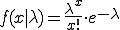 mit
mit
Wir alle kennen das Problem: man geht vergnügt über einen Weg, summt fröhlich vor sich hin, denkt sich nicht böses — und wird auf einmal von einem Pferd totgetreten. Von der Politik wird dieser dramatische, von Pferden begangene Massenmord totgeschwiegen, doch die Wissenschaft hat sich diesem Problem tapfer angenommen. So analysierte bereits Ladislaus von Bortkewitsch unter größter Selbstaufopferung im Jahr 1898 wie viele Soldaten der preußischen Armee pro Jahr und Korps von Pferden totgetreten wurden. Er kam auf den alarmierenden Wert von 0,61 Soldaten. Nun stellt sich die Frage, mit welcher Wahrscheinlichkeit konnte ein Korps in einem Jahr damit rechnen, dass exakt ein Soldat starb?
Lösung: Unser Wert für λ beträgt 0,61. Der Wert für x ist 1. Die Rechnung lautet daher:
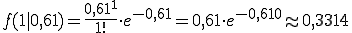 Die Wahrscheinlichkeit, dass exakt ein Soldat in einem Korps in einem bestimmten Jahr von einem bösartigen Pferd totgetreten wurde lag also bei etwa 33,14%.
Die Wahrscheinlichkeit, dass exakt ein Soldat in einem Korps in einem bestimmten Jahr von einem bösartigen Pferd totgetreten wurde lag also bei etwa 33,14%.
Berechnen wir nun auch noch die Wahrscheinlichkeit, dass ein oder mehr Soldaten von Pferden totgetreten wurde (wieder in einem Jahr und Korps):
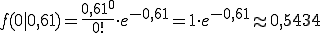 (Zur Erinnerung: es gilt 0! = 1)
(Zur Erinnerung: es gilt 0! = 1)
Es wurde also pro Korps und Jahr mit einer Wahrscheinlichkeit von etwa 54,34% kein Soldat von einem Pferd ermordet. Daraus können wir wiederum ableiten, dass mit einer Wahrscheinlichkeit von 45,66% (berechnet aus 1 - 0,5434) mindestens ein Soldat an den Folgen eines Pferdetritts gestorben ist.
Sowohl der Erwartungswert als auch die Varianz sind bei der Poissonverteilung identisch mit λ. Für das vorherige Beispiel gilt also:
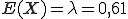
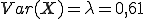
Unter bestimmten Umständen kann man die Poissonverteilung als Ersatz für die Binomialverteilung verwenden. Dafür muss das n (Anzahl der Züge) größer als 100 und das p (die Wahrscheinlichkeit für ein Treffer pro Zug) kleiner als 0,05 sein. Die Berechnung erfolgt dann entsprechend der Definition der Poissonverteilung. Da λ der Erwartungswert ist und für die Binomialverteilung gilt E(X)=np kann λ analog bestimmt werden: λ = np.


- Formel:
für exakt x Treffer und einen vorgegebenen Mittelwert λ.
- Die Poissonverteilung wird häufig zur Berechnung von Wahrscheinlichkeiten in Zeiträumen verwendet, etwa die Wahrscheinlichkeit von x Autounfällen pro Jahr bei λ=10 im Mittel.
- Kann als Ersatz für die Binomialverteilung verwendet werden wenn n>100 und p<0,05. Dann gilt λ=n*p.
1. Definition
Die Poissonverteilung wird in der Regel eingesetzt, um die Wahrscheinlichkeit von Ereignissen innerhalb eines bestimmten Zeitraums zu bestimmen. Beispielsweise könnte man ermitteln, wie wahrscheinlich es ist, dass innerhalb von 5 Minuten x Autos eine bestimmte Kreuzung passieren. Zur Berechnung der Poissonverteilung wird der Erwartungswert als Vorgabe benötigt. Statt E(X) hat es sich allerdings eingebürgert, diesen in der Formel mit λ zu repräsentieren. Die Berechnung erfolgt dann über:
- x: Der Anzahl der Treffer auf die getestet werden soll (exakt x Treffer)
- x!: Der Fakultät von x
- λ: Der Erwartungswert der Verteilung (E(X), muss vorgegeben sein)
- e: Der eulerschen Zahl (ca. 2,718, sollte auf jedem Taschenrechner verfügbar sein)
2. Beispiel
Wir alle kennen das Problem: man geht vergnügt über einen Weg, summt fröhlich vor sich hin, denkt sich nicht böses — und wird auf einmal von einem Pferd totgetreten. Von der Politik wird dieser dramatische, von Pferden begangene Massenmord totgeschwiegen, doch die Wissenschaft hat sich diesem Problem tapfer angenommen. So analysierte bereits Ladislaus von Bortkewitsch unter größter Selbstaufopferung im Jahr 1898 wie viele Soldaten der preußischen Armee pro Jahr und Korps von Pferden totgetreten wurden. Er kam auf den alarmierenden Wert von 0,61 Soldaten. Nun stellt sich die Frage, mit welcher Wahrscheinlichkeit konnte ein Korps in einem Jahr damit rechnen, dass exakt ein Soldat starb?
Lösung: Unser Wert für λ beträgt 0,61. Der Wert für x ist 1. Die Rechnung lautet daher:
Berechnen wir nun auch noch die Wahrscheinlichkeit, dass ein oder mehr Soldaten von Pferden totgetreten wurde (wieder in einem Jahr und Korps):
Es wurde also pro Korps und Jahr mit einer Wahrscheinlichkeit von etwa 54,34% kein Soldat von einem Pferd ermordet. Daraus können wir wiederum ableiten, dass mit einer Wahrscheinlichkeit von 45,66% (berechnet aus 1 - 0,5434) mindestens ein Soldat an den Folgen eines Pferdetritts gestorben ist.
| x (Anzahl totgetretener Soldaten) |
0 | 1 | 2 | 3 |
| f(x|0,61) bzw. Wahrscheinlichkeit (pro Korps und Jahr) |
0,5434 | 0,3314 | 0,1011 | 0,0206 |
3. Erwartungswert und Varianz der Poissonverteilung
Sowohl der Erwartungswert als auch die Varianz sind bei der Poissonverteilung identisch mit λ. Für das vorherige Beispiel gilt also:
4. Poissonverteilung als Ersatz für die Binomialverteilung
Unter bestimmten Umständen kann man die Poissonverteilung als Ersatz für die Binomialverteilung verwenden. Dafür muss das n (Anzahl der Züge) größer als 100 und das p (die Wahrscheinlichkeit für ein Treffer pro Zug) kleiner als 0,05 sein. Die Berechnung erfolgt dann entsprechend der Definition der Poissonverteilung. Da λ der Erwartungswert ist und für die Binomialverteilung gilt E(X)=np kann λ analog bestimmt werden: λ = np.
5. Quiz
Welche Verteilung kann bei n≥100 und p≤0,05 auch über die Poissonverteilung berechnet werden?
Chi-Quadrat-Verteilung
Binomialverteilung
Normalverteilung
Hypergeometrische Verteilung
Angenommen wir haben eine Poissonverteilung mit x=1 und λ=0,881. Wie lautet die Varianz dieser Verteilung?
1,733
0,881
0
1

Kommentare (2)
Von neu nach altWir bitten um ihr Verständnis.
Danke!