Schnellübersicht
Die Normalverteilung ist vermutlich die bekannteste Wahrscheinlichkeitsverteilung. Sie wurde von Carl Friedrich Gauß entwickelt und ist auch besser bekannt als „Glockenkurve”, da die Form des Graphen einer normalverteilten Funktion ähnlich der einer Glocke ist.
Das genaue Aussehen des Graphen ergibt sich aus dem Erwartungswert und der Standardabweichung. (Hinweis: Im Falle der Normalverteilung wird für den Erwartungswert das Zeichen μ (gesprochen „müh”) und für die Standardabweichung das Zeichen σ (gesprochen „sigma”) verwendet.). Vereinfacht ausgedrückt gibt der Erwartungswert (μ) an, wo sich die „Glocke” auf der x-Achse befinden soll (z. B. weit rechts oder weit links vom Ursprung), während die Standardabweichung (σ) die Breite festlegt („plattgedrückt” und damit breit oder stattdessen spitz bzw. schmal). „Standardabweichung” (σ) kann man hier weitestgehend wörtlich nehmen: Wie weit weicht der Graph vom Standard (= der Erwartungswert (μ)) ab? Je größer die Standardabweichung (σ), desto mehr Abweichung und desto breiter ist der Graph.
Die nachfolgende Abbildung vergleicht die Körperlänge von Mäusen und jungen Kätzchen miteinander (jeweils vom Kopf bis zum Anfang des Schwanzes, die Werte sind nur bedingt realistisch). Mäuse sind offensichtlich kleiner als Katzen. Ihre Körpergröße wurde hier auf 9cm geschätzt. Daher beträgt auch der Erwartungswert für die Normalverteilung der Körperlänge von Mäusen 9. Die Körperlänge von Kätzchen ist größer, daher liegt der Erwartungswert bei 16 (entspricht 16cm). Die Körperlänge von Mäusen schwankt etwa zwischen 7 und 11cm, also im Bereich ±2cm. Die Körpergröße von Katzen hingegen schwankt zwischen etwa zwischen 13,3 und 18,7cm (±2,7cm). Entsprechend ist die Standardabweichung der Normalverteilung der Mäuse etwas geringer als bei Katzen, denn die Körpergröße der Mäuse weicht weniger vom Erwartungswert ab. Daraus folgt, dass die Glockenkurve der Mäuse eher spitz und die der Katzen etwas flacher ist.
 Die genaue Formel für die Normalverteilung ist eher kompliziert. Sie lautet:
Die genaue Formel für die Normalverteilung ist eher kompliziert. Sie lautet:
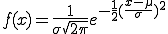 Darin sind μ der Erwartungswert, σ die Standardabweichung und e die eulersche Zahl, welche auf jeden brauchbaren Taschenrechner verfügbar sein sollte.
Darin sind μ der Erwartungswert, σ die Standardabweichung und e die eulersche Zahl, welche auf jeden brauchbaren Taschenrechner verfügbar sein sollte.
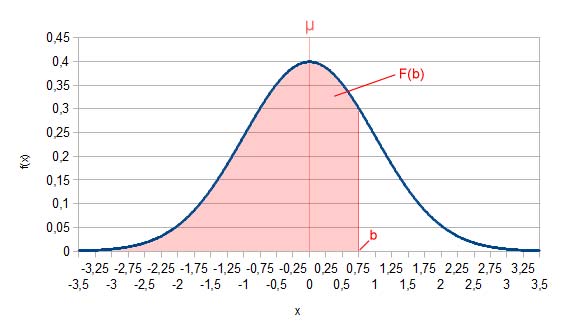
Die Normalverteilung hat einen entscheidenden Unterschied zu allen zuvor vorgestellten Wahrscheinlichkeitsverteilungen: Sie ist stetig statt diskret. Das heißt, dass man für jeden beliebigen x-Wert die Wahrscheinlichkeit bestimmen kann und nicht nur für einige wenige (wie z. B. x=1, x=2, x=3, ...). Dass es unendlich viele Punkte auf dem Graph gibt hat nun den Nachteil, dass die Wahrscheinlichkeit für jeden einzelnen Punkt null ist. Für stetige Wahrscheinlichkeitsverteilungen kann daher nur die Wahrscheinlichkeit von Bereichen bestimmt werden. Es gilt also z. B., dass f(5) = 0 ist, aber f(5 ≤ x ≤ 6) > 0. Wir können also zur Bestimmung von Wahrscheinlichkeiten der Normalverteilung nicht so einfach vorgehen wie bei diskreten Funktionen und einzelne Punkte „herauspicken”. Stattdessen müssen wir Bereiche prüfen — und für die wird ein Integral benötigt:
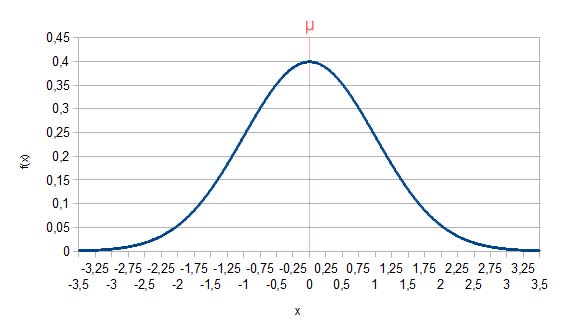
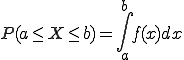 Ähnlich errechnet sich auch die kumulative Verteilungsfunktion, welche alle Wahrscheinlichkeiten bis zu einem bestimmten Wert a auf der x-Achse aufaddiert (und daher konstant ansteigt):
Ähnlich errechnet sich auch die kumulative Verteilungsfunktion, welche alle Wahrscheinlichkeiten bis zu einem bestimmten Wert a auf der x-Achse aufaddiert (und daher konstant ansteigt):
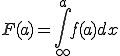
Die zuvor genannten Integrale zu bestimmen ist zeitaufwändig, fehleranfällig — und schlicht nervend. Da ist es wohl nur allzu hilfreich, dass man sie gar nicht bestimmen muss! Stattdessen kann man die Ergebnisse der Integrale mit Hilfe der sogenannten Standardnormalverteilung bestimmen.
Die Standardnormalverteilung ist die Normalverteilung mit Erwartungswert 0 und Standardabweichung 1 (man schreibt auch „N(0, 1)”). Das Vorgehen beim Umrechnen lautet wie folgt:
Zusammenfassend rechnen wir also die x-Werte unserer Normalverteilung so um, dass sie stattdessen auf der Standardnormalverteilung liegen. Die neuen Werte werden als z bezeichnet (optional mit einem Index). Nun können wir jeweils F(z) bestimmen. Die Werte von F(z) können Tabellen entnommen werden, die in jedem Tafelwerk zur Stochastik vorhanden sind. Wohlgemerkt: Diese Umrechnung auf die Standardnormalverteilung ist nicht zwangsweise notwendig. Es ist nur ein kleiner Trick, damit man sich das Bestimmen des Integrals von F(x) sparen kann!
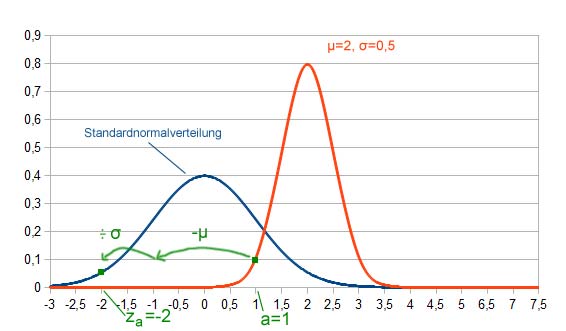
Vielleicht ist nun der Eindruck aufgekommen, dass die Umrechnung auf die z-Werte sehr kompliziert ist, aber weit gefehlt! Das Umrechnen ist stattdessen sehr einfach. Wir müssen nur um μ verschieben und um σ stauchen. Das nachfolgende Bild stellt die Umrechnung dar.
Zuerst wird μ subtrahiert, dann durch σ geteilt.
Die Formel dafür lautet:
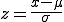
Nun folgt noch eine kurze Tabelle mit einigen Werten von F(z). Weitere Werte sollten sich einem Tafelwerk entnehmen lassen.
Da die Glockenkurve symmetrisch ist werden hier nur die positiven Werte aufgezählt. Die Werte von negativen z-Werten lassen sich über F(-z) = 1 - F(+z) bestimmen.
Nehmen wir an, wir haben eine Normalverteilung, die widerspiegelt, wie viel Kilogramm Menschenfleisch ein durchschnittlicher Zombie an einem beliebigen Tag zu sich nimmt. Der Erwartungswert μ ist 2 und die Standardabweichung σ ist 1,25. Die Verteilung liegt also etwas „rechts” der Standardnormalverteilung (+2) und ist etwas flacher, da es mehr Streuung gibt (1,25 Standardabweichung statt 1,0). Mit welcher Wahrscheinlichkeit nimmt ein Zombie nun zwischen 1,5kg und 2,5kg Menschenfleisch an einem Tag zu sich? Wie viele von 100 zufälligen Zombies nehmen voraussichtlich an einem Tag mehr als 4kg zu sich und wie viele verlieren voraussichtlich Gewicht (x<0 — Zombie verliert mal einen abgefaulten Arm o. ä.)?
Lösung: Bestimmen wir erstmal die Lösung der ersten Frage. Wir wollen die Wahrscheinlichkeit des Bereichs zwischen a=1,5kg und b=2,5kg berechnen. Dazu müssen wir a in za und b in zb umrechnen. Die Formel lautet dazu (wie zuvor beschrieben)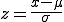 . Die Umrechnung erfolgt also über:
. Die Umrechnung erfolgt also über:
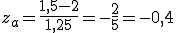
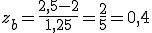 In der weiter zuvor aufgeführten Tabelle ist 0,4 nicht enthalten, daher sei hier gesagt, dass gilt F(0,4)=0,6554 für die Standardnormalverteilung. Daher ist F(za)=1-0,6554=0,3446 und F(zb)=0,6554. Es gilt daher P(1,5 ≤ X ≤ 2,5) = F(zb) - F(za) = 0,6554 - 0,3446 = 0,3108. Die Wahrscheinlichkeit, dass ein Zombie an einem beliebigen Tag zwischen 1,5kg und 2,5kg zu sich nimmt liegt also bei 31,08%. (Die Wahrscheinlichkeit des Bereichs von 1,5kg bis 2,5kg (bei μ=2 und σ=1,25) ist identisch mit der Wahrscheinlichkeit des Bereich von -0,4kg bis +0,4kg bei der Standardnormalverteilung (μ=0 und σ=1).)
In der weiter zuvor aufgeführten Tabelle ist 0,4 nicht enthalten, daher sei hier gesagt, dass gilt F(0,4)=0,6554 für die Standardnormalverteilung. Daher ist F(za)=1-0,6554=0,3446 und F(zb)=0,6554. Es gilt daher P(1,5 ≤ X ≤ 2,5) = F(zb) - F(za) = 0,6554 - 0,3446 = 0,3108. Die Wahrscheinlichkeit, dass ein Zombie an einem beliebigen Tag zwischen 1,5kg und 2,5kg zu sich nimmt liegt also bei 31,08%. (Die Wahrscheinlichkeit des Bereichs von 1,5kg bis 2,5kg (bei μ=2 und σ=1,25) ist identisch mit der Wahrscheinlichkeit des Bereich von -0,4kg bis +0,4kg bei der Standardnormalverteilung (μ=0 und σ=1).)
Nehmen wir uns nun die zweite Frage vor, die lautete: „Wie viele von 100 zufälligen Zombies nehmen voraussichtlich an einem Tag mehr als 4kg zu sich und wie viele verlieren voraussichtlich Gewicht?”
Diesmal gilt also a=4. Da die Wahrscheinlichkeit ≥a berechnet werden soll können wir auch einfach die Gegenwahrscheinlichkeit verwenden und 1 - F(a) rechnen (sprich 100% minus alles bis a). Wir berechnen zunächst za:
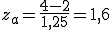 Der Wert F(1,6) für die Standardnormalverteilung ist 0,9452. Daher gilt P(X≥4) = 1 - 0,9452 = 0,0548. Nun wissen wir, dass 5,48% aller Zombies mehr als 4kg Fleisch essen. Auf 100 Zombies umgerechnet heißt das, dass voraussichtlich 5,48 Zombies (gerundet also 5) mehr als 4kg essen werden.
Der Wert F(1,6) für die Standardnormalverteilung ist 0,9452. Daher gilt P(X≥4) = 1 - 0,9452 = 0,0548. Nun wissen wir, dass 5,48% aller Zombies mehr als 4kg Fleisch essen. Auf 100 Zombies umgerechnet heißt das, dass voraussichtlich 5,48 Zombies (gerundet also 5) mehr als 4kg essen werden.
Für die Anzahl der Zombies, die Gewicht verlieren (x<0) gehen wir sehr vergleichbar vor. Es gilt nun a=0, umgerechnet in za:
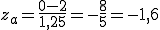 Der Wert F(-1,6) für die Standardnormalverteilung ist 0,0548, womit wieder 5,48 Zombies bzw. gerundet 5 Zombies Gewicht verlieren. Das Ergebnis ist also genauso wie das der vorherigen Rechnung. Das liegt an der Symmetrie der Normalverteilung. Die Bereiche ∞ bis 0kg und 4kg bis ∞ sind jeweils 2kg vom Erwartungswert „entfernt” und sind beide genauso groß, daher sind auch ihre Wahrscheinlichkeiten gleich.
Der Wert F(-1,6) für die Standardnormalverteilung ist 0,0548, womit wieder 5,48 Zombies bzw. gerundet 5 Zombies Gewicht verlieren. Das Ergebnis ist also genauso wie das der vorherigen Rechnung. Das liegt an der Symmetrie der Normalverteilung. Die Bereiche ∞ bis 0kg und 4kg bis ∞ sind jeweils 2kg vom Erwartungswert „entfernt” und sind beide genauso groß, daher sind auch ihre Wahrscheinlichkeiten gleich.
Der Erwartungswert der Normalverteilung ist bereits vorgegeben (μ) und die Varianz lässt sich anhand der Standardabweichung (σ) berechnen mit Var(X) = σ2.
Es gilt als Faustformel das vom Erwartungswert aus im Bereich ±2σ etwa 95% aller Werte liegen und im Bereich ±3σ etwa 99% aller Werte. Im Bezug auf das vorherige Beispiel hieße das etwa, dass 99% aller Zombies in etwa zwischen -1,75kg (2kg-3*1,25kg) und 5,75kg (2kg+3*1,25kg) pro Tag zunehmen.
Im diesem Artikel wurde für „a≤X≤b” in aller Regel der Begriff „Bereich” verwendet. Mathematisch präziser wäre „Intervall”.

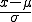
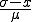
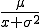
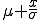



- Besser bekannt als „Glockenkurve”, da der Graph der Verteilung einer Glocke ähnelt.
- Die genaue Form der Normalverteilung wird über den Erwartungswert μ und die Standardabweichung σ bestimmt. Der Erwartungswert bestimmt die Position auf der x-Achse (μ=2 heißt, dass der Hochpunkt bei 2 liegt). Die Standardabweichung bestimmt, ob die Glockenkurve eher flach verläuft (hohes σ) oder spitz (niedriges σ).
- Die Normalverteilung ist stetig (statt diskret). Es werden daher nicht die Wahrscheinlichkeiten von einzelnen Punkten, sondern von Bereichen bestimmt.
- Die Standardnormalverteilung ist die Normalverteilung mit μ=0 und σ=1.
- Die Wahrscheinlichkeit eines Bereichs zwischen den Punkten a und b einer Normalverteilung (P(a≤X≤b)) kann immer anhand eines ähnlichen Bereichs der Standardnormalverteilung bestimmt werden (die Wahrscheinlichkeiten beider Bereiche sind dann identisch). Dafür müssen die Grenzen des Bereichs bei der Standardnormalverteilung aus a und b abgeleitet werden (man spricht dann von za und zb).
- Die Formel zum Umrechnen von a in za lautet
.
- Für die Standardnormalverteilung ist die kumulative Verteilungsfunktion F(x) bekannt. Ihre Ergebnisse für verschiedene Werte können aus existierenden Tabellen (zu finden in Tafelwerken) einfach abgelesen werden.
- Es gilt dann
- P(a ≤ X ≤ b) = F(zb) - F(za)
- P(X ≤ a) = F(za)
- P(X ≥ a) = 1 - F(za)
- P(X ≤ b) = F(zb)
- P(X ≥ b) = 1 - F(zb)
1. Definition
Die Normalverteilung ist vermutlich die bekannteste Wahrscheinlichkeitsverteilung. Sie wurde von Carl Friedrich Gauß entwickelt und ist auch besser bekannt als „Glockenkurve”, da die Form des Graphen einer normalverteilten Funktion ähnlich der einer Glocke ist.
Das genaue Aussehen des Graphen ergibt sich aus dem Erwartungswert und der Standardabweichung. (Hinweis: Im Falle der Normalverteilung wird für den Erwartungswert das Zeichen μ (gesprochen „müh”) und für die Standardabweichung das Zeichen σ (gesprochen „sigma”) verwendet.). Vereinfacht ausgedrückt gibt der Erwartungswert (μ) an, wo sich die „Glocke” auf der x-Achse befinden soll (z. B. weit rechts oder weit links vom Ursprung), während die Standardabweichung (σ) die Breite festlegt („plattgedrückt” und damit breit oder stattdessen spitz bzw. schmal). „Standardabweichung” (σ) kann man hier weitestgehend wörtlich nehmen: Wie weit weicht der Graph vom Standard (= der Erwartungswert (μ)) ab? Je größer die Standardabweichung (σ), desto mehr Abweichung und desto breiter ist der Graph.
Die nachfolgende Abbildung vergleicht die Körperlänge von Mäusen und jungen Kätzchen miteinander (jeweils vom Kopf bis zum Anfang des Schwanzes, die Werte sind nur bedingt realistisch). Mäuse sind offensichtlich kleiner als Katzen. Ihre Körpergröße wurde hier auf 9cm geschätzt. Daher beträgt auch der Erwartungswert für die Normalverteilung der Körperlänge von Mäusen 9. Die Körperlänge von Kätzchen ist größer, daher liegt der Erwartungswert bei 16 (entspricht 16cm). Die Körperlänge von Mäusen schwankt etwa zwischen 7 und 11cm, also im Bereich ±2cm. Die Körpergröße von Katzen hingegen schwankt zwischen etwa zwischen 13,3 und 18,7cm (±2,7cm). Entsprechend ist die Standardabweichung der Normalverteilung der Mäuse etwas geringer als bei Katzen, denn die Körpergröße der Mäuse weicht weniger vom Erwartungswert ab. Daraus folgt, dass die Glockenkurve der Mäuse eher spitz und die der Katzen etwas flacher ist.
Hinweis: Die Formeln im nachfolgenden Abschnitt müssen nicht auswendig gelernt werden! (Siehe dazu auch das nächste Kapitel)
Die Normalverteilung hat einen entscheidenden Unterschied zu allen zuvor vorgestellten Wahrscheinlichkeitsverteilungen: Sie ist stetig statt diskret. Das heißt, dass man für jeden beliebigen x-Wert die Wahrscheinlichkeit bestimmen kann und nicht nur für einige wenige (wie z. B. x=1, x=2, x=3, ...). Dass es unendlich viele Punkte auf dem Graph gibt hat nun den Nachteil, dass die Wahrscheinlichkeit für jeden einzelnen Punkt null ist. Für stetige Wahrscheinlichkeitsverteilungen kann daher nur die Wahrscheinlichkeit von Bereichen bestimmt werden. Es gilt also z. B., dass f(5) = 0 ist, aber f(5 ≤ x ≤ 6) > 0. Wir können also zur Bestimmung von Wahrscheinlichkeiten der Normalverteilung nicht so einfach vorgehen wie bei diskreten Funktionen und einzelne Punkte „herauspicken”. Stattdessen müssen wir Bereiche prüfen — und für die wird ein Integral benötigt:
2. Berechnung über Standardnormalverteilung
Die zuvor genannten Integrale zu bestimmen ist zeitaufwändig, fehleranfällig — und schlicht nervend. Da ist es wohl nur allzu hilfreich, dass man sie gar nicht bestimmen muss! Stattdessen kann man die Ergebnisse der Integrale mit Hilfe der sogenannten Standardnormalverteilung bestimmen.
Die Standardnormalverteilung ist die Normalverteilung mit Erwartungswert 0 und Standardabweichung 1 (man schreibt auch „N(0, 1)”). Das Vorgehen beim Umrechnen lautet wie folgt:
- Es liegt eine Normalverteilung vor für die man die Wahrscheinlichkeit eines bestimmten Bereichs zwischen a und b bestimmen will
- Man errechnet, an welchen x-Werten a und b bei der Standardnormalverteilung liegen würden. Dazu muss man sie in der Regel zuerst um den Erwartungswert verschieben (da für die Standardnormalverteilung gilt μ=0) und danach um die Standardabweichung stauchen (da aller Wahrscheinlichkeit nach die Standardnormalverteilung „breiter” oder „schmaler” ist als die Normalverteilung für die man die Wahrscheinlichkeit bestimmen will). Die neuen Werte werden als za und zb bezeichnet.
- Man bestimmt F(za) und F(zb). Diese können einfach aus bereits vorgefertigten Tabellen abgelesen werden.
- Es gilt nun P(a ≤ X ≤ b) = F(zb) - F(za). Wieso genau F(zb) - F(za)? Weil F(zb) die Wahrscheinlichkeit aller Werte bis b zusammengerechnet bestimmt (-∞ bis b), während F(za) die Wahrscheinlichkeit aller Werte bis a zusammengerechnet bestimmt (-∞ bis a). Den Bereich zwischen -∞ und a wollen wir hier nicht beachten, daher wird er subtrahiert und wir erhalten den Bereich a bis b.
Zusammenfassend rechnen wir also die x-Werte unserer Normalverteilung so um, dass sie stattdessen auf der Standardnormalverteilung liegen. Die neuen Werte werden als z bezeichnet (optional mit einem Index). Nun können wir jeweils F(z) bestimmen. Die Werte von F(z) können Tabellen entnommen werden, die in jedem Tafelwerk zur Stochastik vorhanden sind. Wohlgemerkt: Diese Umrechnung auf die Standardnormalverteilung ist nicht zwangsweise notwendig. Es ist nur ein kleiner Trick, damit man sich das Bestimmen des Integrals von F(x) sparen kann!
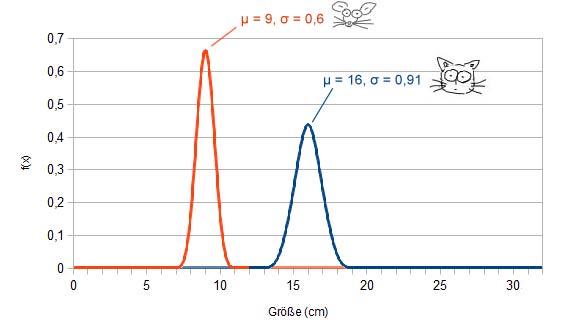
Vielleicht ist nun der Eindruck aufgekommen, dass die Umrechnung auf die z-Werte sehr kompliziert ist, aber weit gefehlt! Das Umrechnen ist stattdessen sehr einfach. Wir müssen nur um μ verschieben und um σ stauchen. Das nachfolgende Bild stellt die Umrechnung dar.
Zuerst wird μ subtrahiert, dann durch σ geteilt.
Die Formel dafür lautet:
Nun folgt noch eine kurze Tabelle mit einigen Werten von F(z). Weitere Werte sollten sich einem Tafelwerk entnehmen lassen.
| z | F(z) |
|---|---|
| 0,00 | 0,5000 |
| 0,25 | 0,5987 |
| 0,50 | 0,6914 |
| 0,75 | 0,7733 |
| 1,00 | 0,8413 |
| 1,25 | 0,8943 |
| 1,50 | 0,9331 |
| 1,75 | 0,9599 |
| 2,00 | 0,9772 |
| 2,25 | 0,9877 |
| 2,50 | 0,9937 |
| 2,75 | 0,9970 |
| 3,00 | 0,9986 |
3. Beispiel
Nehmen wir an, wir haben eine Normalverteilung, die widerspiegelt, wie viel Kilogramm Menschenfleisch ein durchschnittlicher Zombie an einem beliebigen Tag zu sich nimmt. Der Erwartungswert μ ist 2 und die Standardabweichung σ ist 1,25. Die Verteilung liegt also etwas „rechts” der Standardnormalverteilung (+2) und ist etwas flacher, da es mehr Streuung gibt (1,25 Standardabweichung statt 1,0). Mit welcher Wahrscheinlichkeit nimmt ein Zombie nun zwischen 1,5kg und 2,5kg Menschenfleisch an einem Tag zu sich? Wie viele von 100 zufälligen Zombies nehmen voraussichtlich an einem Tag mehr als 4kg zu sich und wie viele verlieren voraussichtlich Gewicht (x<0 — Zombie verliert mal einen abgefaulten Arm o. ä.)?
Lösung: Bestimmen wir erstmal die Lösung der ersten Frage. Wir wollen die Wahrscheinlichkeit des Bereichs zwischen a=1,5kg und b=2,5kg berechnen. Dazu müssen wir a in za und b in zb umrechnen. Die Formel lautet dazu (wie zuvor beschrieben)
Nehmen wir uns nun die zweite Frage vor, die lautete: „Wie viele von 100 zufälligen Zombies nehmen voraussichtlich an einem Tag mehr als 4kg zu sich und wie viele verlieren voraussichtlich Gewicht?”
Diesmal gilt also a=4. Da die Wahrscheinlichkeit ≥a berechnet werden soll können wir auch einfach die Gegenwahrscheinlichkeit verwenden und 1 - F(a) rechnen (sprich 100% minus alles bis a). Wir berechnen zunächst za:
Für die Anzahl der Zombies, die Gewicht verlieren (x<0) gehen wir sehr vergleichbar vor. Es gilt nun a=0, umgerechnet in za:
4. Erwartungswert, Varianz
Der Erwartungswert der Normalverteilung ist bereits vorgegeben (μ) und die Varianz lässt sich anhand der Standardabweichung (σ) berechnen mit Var(X) = σ2.
5. Anmerkungen
Es gilt als Faustformel das vom Erwartungswert aus im Bereich ±2σ etwa 95% aller Werte liegen und im Bereich ±3σ etwa 99% aller Werte. Im Bezug auf das vorherige Beispiel hieße das etwa, dass 99% aller Zombies in etwa zwischen -1,75kg (2kg-3*1,25kg) und 5,75kg (2kg+3*1,25kg) pro Tag zunehmen.
Im diesem Artikel wurde für „a≤X≤b” in aller Regel der Begriff „Bereich” verwendet. Mathematisch präziser wäre „Intervall”.
6. Quiz
Wie wird ein Wert einer Normalverteilung mit dem Erwartungswert μ und der Standardabweichung σ in seinen passenden z-Wert umgerechnet?
Angenommen es liegen a und b vor. Aus diesen wurden bereits za und zb der Standardnormalverteilung berechnet. Wie errechnet sich nun die Wahrscheinlichkeit P(a ≤ X ≤ b), wenn F(x) die kumulative Verteilungsfunktion der Standardnormalverteilung ist?
1 - F(zb)
F(zb) - F(za)
1 - F(za)
F(za) + F(zb)
Wenn eine Normalverteilung den Wert μ=7 und σ=2 hat, wie lautet dann der x-Wert a=3 umgerechnet in za?
7
-2
0
-1
Angenommen es liegt eine Normalverteilung vor mit μ=5 und σ=1,33. Wie lautet das Ergebnis von F(∞) für diese Verteilung?
0
1
1,33
100
7. Links
- Lernmaterialien in Wikibooks, inklusive Übungsaufgaben
- Allgemeine Einführung in Normalverteilungen (Khan Acadamy, Video, englisch)
- Mehr zum Rechnen mit Normalverteilungen sowie Unterschiede zwischen diskreten und stetigen Verteilungen (Khan Acadamy, Video, englisch)
- Skript zum Bereichen von Wahrscheinlichkeiten in Intervallen (nur zum Üben, ja?!)
- Herleitung der Normalverteilung aus der Binomialverteilung
- Applet zum Visualisieren der Graphen von Normalverteilungen (englisch)
- Detailliertere Tabelle mit den Werten der kumulativen Verteilungsfunktion für die Standardnormalverteilung (englisch)
Kommentare (6)
Von neu nach altWir bitten um ihr Verständnis.
Danke!
ich wollte nur noch einmal ein fettes Dankeschön loswerden!
Ich mache gerade ein Austauschjahr in Finnland und Matte auf finnisch ist dann doch etwas schwieriger zu verstehen. ;)
Diese Seite hat mich gerettet.
Danke
Muss es nicht
" P(a ≤ X ≤ b) = F(zb) - F(za). Wieso genau F(zb) - F(za)? Weil F(zb))..."
lauten?
Ansonsten guter Beitrag!