Erwartungswert, Varianz und Standardabweichung (Stochastik)

Schnellübersicht

Erwartungswert = der Wert, der nach vielen Wiederholungen eines Zufallsexperiments am ehesten „im Durchschnitt” zu erwarten ist
Formel Erwartungswert: $Formel-Code: E(X) = x_1 \cdot P(X=x_1) + x_2 \cdot P(X=x_2) + ... + x_n \cdot P(X=x_n)$ (X ist eine Zufallsvariable, P(X) eine Wahrscheinlichkeitsverteilung)
Varianz = Maß für die Streuung einer Zufallsvariablen (um den Erwartungswert)
Formel Varianz:
Standardabweichung = Genauso wie Varianz ebenfalls ein Maß für die Streuung, errechnet sich aus der Varianz
Formel Standardabweichung: $Formel-Code: \sigma(X) = \sqrt{Var(X)}$

1. Definition

Der Erwartungswert wird auf eine Wahrscheinlichkeitsverteilung angewendet und ermittelt den Wert, der bei sehr häufiger Wiederholung des Zufallsexperiments am ehesten als Mittelwert zu erwarten ist (daher der Name „Erwartungswert”). Das Gesetz der großen Zahl gewährleistet, dass sich dieser Wert nach vielen Wiederholungen ungefähr ergibt — bei nur sehr wenigen Wiederholungen gibt es aber eine hohe Schwankungsbreite.
Ist die Zufallsvariable X und die Wahrscheinlichkeitsverteilung P(X) gegeben, dann wird der Erwartungswert ermittelt über

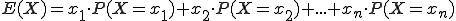$Formel-Code: E(X) = x_1 \cdot P(X=x_1) + x_2 \cdot P(X=x_2) + ... + x_n \cdot P(X=x_n)$

Häufig schreibt man auch kurz μ statt E(X).

2. Beispiel: Anwendung auf Würfelwurf

Wir definieren für den Wurf eines Würfels den Ergebnisraum Ω = {1, 2, 3, 4, 5, 6}, die Zufallsvariable X(ω)=ω (heißt: die Zufallsvariable bildet die Augenzahl auf den selben Wert ab, also 1 auf 1, 2 auf 2 usw.) und die Wahrscheinlichkeitsverteilung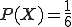 $Formel-Code: P(X) = \frac{1}{6}$ (jede Augenzahl hat also die Wahrscheinlichkeit 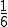$Formel-Code: \frac{1}{6}$ ). Der Erwartungswert ergibt sich nun über:

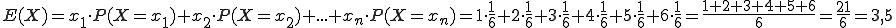$Formel-Code: E(X) = x_1 \cdot P(X=x_1) + x_2 \cdot P(X=x_2) + ... + x_n \cdot P(X=x_n) = 1 \cdot \frac{1}{6} + 2 \cdot \frac{1}{6} + 3 \cdot \frac{1}{6} + 4 \cdot \frac{1}{6} + 5 \cdot \frac{1}{6} + 6 \cdot \frac{1}{6} = \frac{1+2+3+4+5+6}{6} = \frac{21}{6} = 3,5$

Der Wert, der sich nach vielen Würfelwürfen also im Mittel ergeben wird ist 3,5.

3. Beispiel: Anwendung auf doppelten Würfelwurf

Für das nächste Beispiel wollen wir zwei Würfel werfen und die Augenzahl der beiden jeweils addieren. Über den Erwartungswert kann bestimmt werden, welche (addierte) Augenzahl am ehesten erwartet werden kann (nach vielen Wiederholungen). Bereits im Artikel zur Wahrscheinlichkeitsverteilung wurde auf den doppelten Würfelwurf eingegangen. Daher sei hier nur die Tabelle mit den Werten der Zufallsvariablen und den zugehörigen Wahrscheinlichkeiten aufgelistet:

xi	2	3	4	5	6	7	8	9	10	11	12
P(X = xi)	$Formel-Code: \frac{1}{36}$	$Formel-Code: \frac{2}{36}$	$Formel-Code: \frac{3}{36}$	$Formel-Code: \frac{4}{36}$	$Formel-Code: \frac{5}{36}$	$Formel-Code: \frac{6}{36}$	$Formel-Code: \frac{5}{36}$	$Formel-Code: \frac{4}{36}$	$Formel-Code: \frac{3}{36}$	$Formel-Code: \frac{2}{36}$	$Formel-Code: \frac{1}{36}$

Der Erwartungswert kann daher wie folgt berechnet werden:

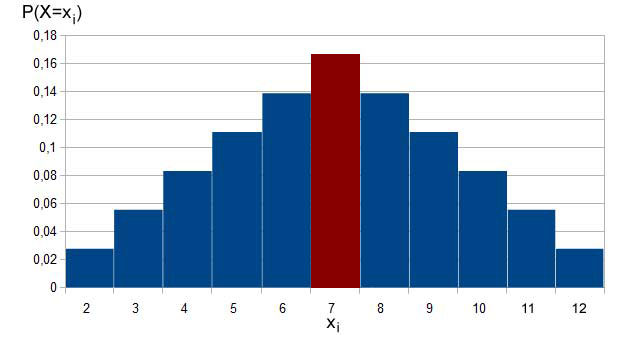
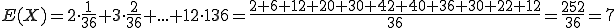$Formel-Code: E(X) = 2 \cdot \frac{1}{36} + 3 \cdot \frac{2}{36} + ... + 12 \cdot {1}{36} = \frac{2+6+12+20+30+42+40+36+30+22+12}{36} = \frac{252}{36} = 7$

Bei genügend Würfen mit zwei Würfeln wird also am häufigsten als Summe der Augenzahlen die 7 erscheinen. Im Histogramm ist der Bereich markiert:

Histogramm zum doppelten Würfelwurf.
Rot markiert ist der Bereich des Erwartungswerts (7).

4. Der Erwartungswert und Glücksspiele

Der Erwartungswert lässt sich gut auf Glücksspiele anwenden, um den zu erwartenden Gewinn oder Verlust zu berechnen. Dazu muss der Gewinn und Verlust als Zufallsvariable ausgedrückt werden und eine Wahrscheinlichkeitsverteilung vorliegen, die den jeweiligen Gewinnen und Verlusten eine Wahrscheinlichkeit zuordnet.

Beispiel 1: Nehmen wir etwa an, dass für ein Gewinnspiel eine Katze aus dem zehnten Stock eines Hauses geworfen wird. Vor jedem Wurf muss 10 Euro Einsatz gezahlt werden. Landet die Katze auf ihren Pfoten, dann verliert der Werfer seinen Einsatz. Landet sie auf dem Rücken, dann erhält er den Einsatz zurück und zusätzlich 30 Euro. Aus umfangreichen Experimenten ist nun bekannt, dass Katzen bei dieser Höhe in etwa 70% aller Fälle auf den Pfoten landen. Mit welchen Gewinn oder Verlust kann der Werfer am ehesten rechnen?
Lösung: Definieren wir die Zufallsvariable X so, dass sie dem Elementarereignis „Landet auf Pfoten” eine -10 (für 10 Euro Einsatz verloren) und dem Elementarereignis „Landet auf Rücken” eine +30 (für 30 Euro Gewinn) zuweist. Definieren wir ferner P(X=xi) so, dass P(X=-10) = 0,7 und P(X=30) = 0,3 gilt. Der Erwartungswert ist dann:

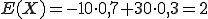$Formel-Code: E(X) = -10 \cdot 0,7 + 30 \cdot 0,3 = 2$

Das heißt, dass der Werfer pro Spiel mit ungefähr 2 Euro Gewinn rechnen kann. (Das freut den Werfer, aber nicht die Katzen.)

Beispiel 2: Wählen wir als zweites Beispiel ein vereinfachtes Lotto. Dabei gewinnt der Spieler nur wenn er 6 richtige hat (Zusatzzahl wird ignoriert). Wenn er gewinnt, dann ist der Gewinn eine Million Euro. Pro ausgefüllten Schein wird 1 Euro berechnet. Mit welchen Gewinn oder Verlust kann der Spieler pro Spiel rechnen?
Lösung: Die Wahrscheinlichkeit, eine richtige Reihe (also eine mit sechs richtigen) zu tippen liegt bei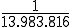 $Formel-Code: \frac{1}{13.983.816}$ (siehe dazu den Artikel Kombination). Definieren wir die Zufallsvariable X nun so, dass sie dem Elementarereignis „nicht sechs richtige” eine -1 und dem Elementarereignis „sechs richtige” die Zahl 1.000.000 zuweist (den 1 Euro verlorenen Einsatz ignorieren wir mal beim Hauptgewinn). 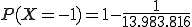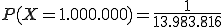Es sei zudem die Wahrscheinlichkeitsverteilung definiert als $Formel-Code: P(X=-1) = 1 - \frac{1}{13.983.816}$ und $Formel-Code: P(X=1.000.000) = \frac{1}{13.983.816}$ . Der Erwartungswert berechnet sich dann wie folgt:

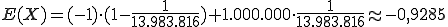$Formel-Code: E(X) = (-1)\cdot (1 - \frac{1}{13.983.816}) + 1.000.000 \cdot \frac{1}{13.983.816} \approx -0,9285$

Langfristig verliert man also bei diesem vereinfachten Lotto etwa 0,93€ pro Schein und damit mehr als 90% seines Einsatzes. Da sollte man doch besser einige Katzen werfen!

4.1. Günstig/ungünstig für den Spieler oder fair

Abhängig vom Erwartungswert werden Glücksspiele in drei verschiedene Kategorien eingeteilt:

Für den Spieler günstige Spiele: Bei diesen Spielen kann der Spieler damit rechnen, langfristig zu gewinnen. Diese Spiele sollte er bei Möglichkeit spielen. Es gilt für den Erwartungswert: E(X) > 0.
Faire Spiele: Bei diesen Spielen gewinnt der Spieler langfristig nicht, verliert aber auch nicht. Der Erwartungswert ist bei diesen Spielen gleich 0 (E(X)=0).
Für den Spieler ungünstige Spiele: Diese Spiele sollte der Spieler meiden. Der Erwartungswert ist kleiner als 0: E(X) < 0. Das heißt, dass der Spieler langfristig beim Spielen dieser Spiele verliert. Letztlich haben alle heutigen Glücksspiele einen Erwartungswert kleiner als 0 und sollten daher nicht gespielt werden.

5. Varianz

Der Erwartungswert gibt nur an, welcher Wert langfristig am ehesten zu erwarten ist. Es handelt sich immer um einen einzelnen Wert. Wir werden aber in der Regel weitere Elementarereignisse beim Durchführung des Zufallsexperiments erhalten — und viele davon werden möglicherweise ebenfalls sehr wahrscheinlich sein. Beispielsweise könnten wir uns einen fiktiven Würfel vorstellen, bei dem die Augenzahl 1 eine Wahrscheinlichkeit von 50% hat und die Augenzahl 6 ebenfalls 50%. Der Erwartungswert würde dann wieder in der Mitte zwischen den beiden Augenzahlen liegen, wäre aber nicht repräsentativ. Eine derartige zu erwartende Abweichungen vom Erwartungswert wird als Streuung bezeichnet. Bei geringer Streuung ist davon auszugehen, dass sich zumeist Werte nahe dem Erwartungswert ergeben werden. Bei hoher Streuung hingegen werden viele Werte abseits des Erwartungswerts liegen. Die Streuung wird mittels der sogenannten Varianz berechnet. Die Formel für die Varianz lautet:

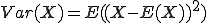Es wird also zunächst der Erwartungswert benötigt. Dieser wird von jedem Wert abgezogen. Das Ergebnis wird quadriert. Über all diese Ergebnisse wird dann wiederum der Erwartungswert gebildet. Die Quadrierung bewirkt, dass Werte, die recht weit vom Erwartungswert entfernt sind (durch das -E(X)) und die dennoch wahrscheinlich sind besonders stark zählen. Es dient sozusagen zum Erkennen von „Ausreißern”.
Da E(X) auch als μ bezeichnet wird schreibt man die Varianz häufig wie folgt:

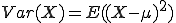
$Formel-Code: Var(X) = E((X - \mu)^2)$

Hinweis zur Berechnung: Es wird jeweils vom Wert xi der Zufallsvariablen zuerst der Erwartungswert E(X) abgezogen, dieses Ergebnis dann quadriert und das ganze dann wiederum mit der Wahrscheinlichkeit P(X = xi) multipliziert. (Entsprechend verfährt man mit jedem Wert xi und summiert wiederum die einzelnen Ergebnisse am Ende.) Siehe dazu auch das nachfolgende Beispiel. Die Formel lässt sich daher auch wie folgt schreiben:

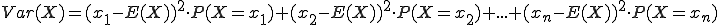
$Formel-Code: Var(X) = (x_1 - E(X))^2 \cdot P(X=x_1) + (x_2 - E(X))^2 \cdot P(X=x_2) + ... + (x_n - E(X))^2 \cdot P(X=x_n)$

5.1. Beispiel zur Varianz: Würfelwurf

Berechnen wir zunächst die Varianz des normalen Würfelwurfs. Wir haben bereits weiter oben berechnet, dass der Erwartungswert E(X) für den Würfelwurf 3,5 ist. Die Varianz berechnet sich nun wie folgt:

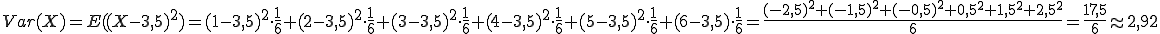$Formel-Code: Var(X) = E((X - 3,5)^2) = (1-3,5)^2 \cdot \frac{1}{6} + (2-3,5)^2 \cdot \frac{1}{6} + (3-3,5)^2 \cdot \frac{1}{6} + (4-3,5)^2 \cdot \frac{1}{6} + (5-3,5)^2 \cdot \frac{1}{6} + (6-3,5) \cdot \frac{1}{6} = \frac{(-2,5)^2 + (-1,5)^2 + (-0,5)^2 + 0,5^2 + 1,5^2 + 2,5^2}{6} = \frac{17,5}{6} \approx 2,92$

Die Varianz für den Würfelwurf liegt also bei 2,92. Das spiegelt die Tatsache wider, dass jede Seite des Würfels die selbe Wahrscheinlichkeit besitzt und die Streuung daher sehr hoch ist.

6. Standardabweichung

Die Standardabweichung (Zeichen: σ, kleines Sigma) ist nichts anderes als die Wurzel aus der Varianz:

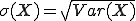$Formel-Code: \sigma(X) = \sqrt{Var(X)}$

Damit ist die Standardabweichung ebenfalls ein Maß für die Streuung, nur dass sie etwas langsamer ansteigt als die Varianz. Kennt man die Varianz, dann kann diese leicht in die Standardabweichung umgerechnet werden (und umgekehrt).

7. Quiz

Über welche der nachfolgenden Formeln wird der Erwartungswert berechnet?

$Formel-Code: E(X) = \frac{x_1}{P(X=x_1)} + \frac{x_2}{P(X=x_2)} + ... + \frac{x_n}{P(X=x_n)}$

$Formel-Code: E(X) = x_1 \cdot P(X=x_1) + x_2 \cdot P(X=x_2) + ... + x_n \cdot P(X=x_n)$

#7018

Mit welchem Zeichen wird der Erwartungswert auch häufig abgekürzt?

#7019

Wie errechnet sich die Varianz?

#7020

Welches Zeichen repräsentiert die Standardabweichung?

#7021

Wie errechnet sich die Standardabweichung aus der Varianz?

$Formel-Code: Var(X) \cdot \sqrt{Var(X)}$

$Formel-Code: \frac{1}{Var(X)}$

$Formel-Code: \sqrt{Var(X)}$

#7022

Kommentare (11)

Von neu nach alt

Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.

wie kann man den Erwartungswert in folgenden Beispiel berechnen.
man wirft 2 W6 Würfel und legt den mit den niedriegeren Wert weg.
Der Wert muss ja höher als 3,5 sein. Aber niedriger als sechs.
Kann mir jemand helfen?

Sehr gute Erklärung, sehr geniales Beispiel ;D

super Erklärung! Aber das Beispiel mit der Katze geht ja mal gar nicht :/

mit Abstand die beste Erklärung der Varianz, die mir bis jetzt untergekommen ist

krass gut erklärt aber es geht noch besser

super

super Hilfe. Danke

Schon wieder muss die Arme Katze als Beispiel herhalten :D

gut erklärt

Alle Kommentare zeigen (11)

Erwartungswert, Varianz und Standardabweichung (Thema: Stochastik)

Einführung zum Begriff "Erwartungswert" und wie dieser aus einer Zufallsvariablen und einer Wahrscheinlichkeitsverteilung berechnet wird. Anwendung auf Glücksspiele wird beschrieben. Ebenfalls erklärt werden die Varianz und die Standardabweichung.