Schnellübersicht
Die sogenannte Vierfeldertafel (auch Vier-Felder-Tafel) ist eine Tabelle in der Werte für absolute und relative Häufigkeiten eingetragen werden. (Nachfolgend wird nur die Anwendung für relative Häufigkeiten erklärt. Die Anwendung für absolute Häufigkeiten ist praktisch identisch.)
Die Werte in der Vierfeldertafel spiegeln zwei gemessene Merkmale wider, welche wiederum jeweils gelten oder nicht gelten können. Es ergeben sich dadurch im inneren Bereich vier Felder nach denen die Vierfeldertafel benannt ist:
Die Vierfeldertafel hat zwei entscheidende Vorteile: erstens hilft sie dabei, eine Menge von Ergebnissen oder Vorgaben übersichtlicher zu gestalten, zum anderen vereinfacht sie das Bestimmen neuer Werte aus den bereits vorhandenen.
Als Randsummen werden — wie der Name schon sagt — die Werte an den Rändern der Vierfeldertafel bezeichnet. Diese (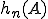 ,
, 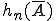 ,
, 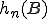 ,
, 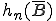 ) ergeben sich jeweils aus der Addition der Werte im inneren Bereich der Tabelle, die in der selben Reihe oder Spalte liegen wie die Randsumme. In den folgenden beiden Abbildungen wird diese Summierung dargestellt. In der ersten wird die Bestimmung von
) ergeben sich jeweils aus der Addition der Werte im inneren Bereich der Tabelle, die in der selben Reihe oder Spalte liegen wie die Randsumme. In den folgenden beiden Abbildungen wird diese Summierung dargestellt. In der ersten wird die Bestimmung von 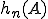 sowie von
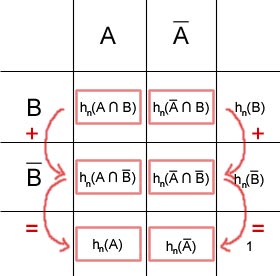
sowie von 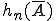 gezeigt, in der zweiten entsprechend
gezeigt, in der zweiten entsprechend 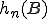 und
und 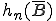 . Es gilt beispielsweise
. Es gilt beispielsweise 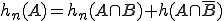 .
.
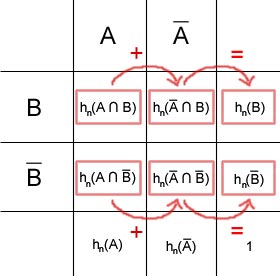
Aus dieser Möglichkeit der Summenbildung folgt auch, dass in jeder Spalte oder Reihe in der zwei Werte bekannt sind der dritte errechnet werden kann.
Genauso wie die Spalten und Reihen summiert die Randsumme geben, können auch die Randsummen wiederum aufsummiert werden und ergeben immer 1. Das heißt, dass gilt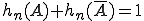 und
und 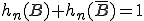 .
.
Nehmen wir an, dass in umfangreichen wissenschaftlichen Experimenten 800 Kätzchen mit brauner und schwarzer Fellfarbe darauf untersucht wurden, ob diese in friedlicher Koexistenz mit Vasen leben können. Dabei wurde herausgefunden, dass 19,6% all dieser Katzen offenbar die Vasen mit Mäusen verwechseln, was zu einer erheblichen Verringerung der „Lebenserwartung” besagter Vasen führt. Bei genauerer Beobachtung wurde ermittelt, dass die braun gefärbten Katzen eine besondere Neigung zu diesem Verhalten zeigen. Insgesamt gelten unter ihnen 12,2% als Vasenumschmeißer. Wie hoch ist der Anteil der schwarzen Katzen, die keine Vasenumschmeißer sind? (Hinweis: Die Anzahl der braunen Katzen wird später noch gezählt (siehe unterhalb der zweiten Abbildung).)
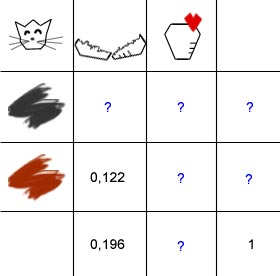
Tragen wir zunächst die bekannten Werte ein. Es gibt das Merkmal „Fellfarbe” (schwarz, braun) und das Merkmal „Beziehung zu Vasen” (Vasenumschmeißer, Vasenliebhaber). Es gilt h800(Vasenumschmeißer) = 0,196 und h800(braun ∩ Vasenumschmeißer) = 0,122. Die Ausgangstabelle lautet demnach:
Da wir wissen, dass sich die Wahrscheinlichkeiten für den Wert, dass eine Katze eine Vasenumschmeißer-Katze ist zu 19,6% addieren und auf braune Katzen bereits 12,2% entfallen muss gelten:
h800(schwarz ∩ Vasenumschmeißer) = h800(Vasenumschmeißer) - h800(braun ∩ Vasenumschmeißer) = 0,196 - 0,122 = 0,074.
Es neigen also 7,4% der schwarzen Katzen zum Umschmeißen von Vasen. Wir wissen ferner, dass sich der Anteil der Vasenumschmeißer und der der Vasenliebhaber zu 100% bzw. 1 addieren muss. Es gilt also
h800(Vasenliebhaber) = 1 - h800(Vasenumschmeißer) = 1 - 0,196 = 0,756,
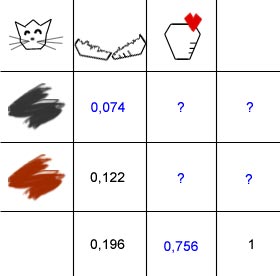
was 75,6% entspricht. Tragen wir diese Werte zunächst in die Tabelle ein:
Nun kommen wir nicht mehr recht weiter, da wir nichts über die Verteilungen der Fellfarben wissen. Einer der Wissenschaftler unterbicht daher seine Dauerkaffepause und kann nach kurzer Zeit berichten, dass 287 der 800 Katzen braun sind. Der Anteil der braunen Katzen liegt demnach bei (287/800) = 0,35875 bzw. 35,875%. Da wir wissen, dass h800(braun ∩ Vasenumschmeißer) = 0,122 gilt demnach
h800(braun ∩ Vasenliebhaber) = h800(braun) - h800(braun ∩ Vasenumschmeißer) = 0,35875 - 0,122 = 0,23675.
Da sich der Anteil der schwarzen und der braunen Katzen zu 100% bzw. 1 addiert wissen wir zudem, dass gilt
h800(schwarz) = 1 - h800(braun) = 1 - 0,35875 = 0,64125.
Nun können wir auch das letzte Feld, nämlich den Anteil der schwarzen Katzen, die Vasenliebhaber sind, errechnen:
h800(schwarz ∩ Vasenliebhaber) = h800(schwarz) - h800(schwarz ∩ Vasenumschmeißer) = 0,64125 - 0,074 = 0,56725.
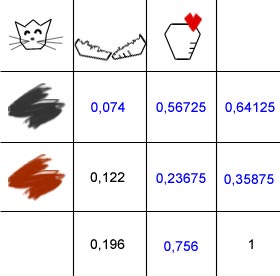
Tragen wir nun die neuen Werte ein:




- Die Vierfeldertafel erfasst relative oder absolute Häufigkeiten, welche nach zwei Merkmalen unterschieden werden (es gilt dann Merkmal A oder nicht A und Merkmal B oder nicht B).
- Es gibt zwei Spalten für Merkmal A (A und nicht A) und zwei Reihen für Merkmal B (B und nicht B).
- Es gibt daher vier Felder im Inneren der Tabelle, welche folgende Werte widerspiegeln (jeweils relative Häufigkeit von ... oder absolute Häufigkeit von ...): A ∩ B, A ∩ nicht B, nicht A ∩ B und nicht A ∩ nicht B.
- Die Werte einer Spalte oder Reihe können aufsummiert werden, um die Randsumme zu erhalten. Es gilt beispielsweise (für die relative Häufigkeit): hn(A ∩ B) = hn(A ∩ B) + hn(A ∩ nicht B)
1. Einleitung
Die sogenannte Vierfeldertafel (auch Vier-Felder-Tafel) ist eine Tabelle in der Werte für absolute und relative Häufigkeiten eingetragen werden. (Nachfolgend wird nur die Anwendung für relative Häufigkeiten erklärt. Die Anwendung für absolute Häufigkeiten ist praktisch identisch.)
| Summe | |||
| Summe | 1 |
Die Werte in der Vierfeldertafel spiegeln zwei gemessene Merkmale wider, welche wiederum jeweils gelten oder nicht gelten können. Es ergeben sich dadurch im inneren Bereich vier Felder nach denen die Vierfeldertafel benannt ist:
- A gilt und B gilt (
)
- A gilt und B gilt nicht (
)
- A gilt nicht und B gilt (
)
- A gilt nicht und B gilt nicht (
)
Die Vierfeldertafel hat zwei entscheidende Vorteile: erstens hilft sie dabei, eine Menge von Ergebnissen oder Vorgaben übersichtlicher zu gestalten, zum anderen vereinfacht sie das Bestimmen neuer Werte aus den bereits vorhandenen.
2. Randsummen und Anwendung
Als Randsummen werden — wie der Name schon sagt — die Werte an den Rändern der Vierfeldertafel bezeichnet. Diese (
Aus dieser Möglichkeit der Summenbildung folgt auch, dass in jeder Spalte oder Reihe in der zwei Werte bekannt sind der dritte errechnet werden kann.
Genauso wie die Spalten und Reihen summiert die Randsumme geben, können auch die Randsummen wiederum aufsummiert werden und ergeben immer 1. Das heißt, dass gilt
3. Beispiel
Nehmen wir an, dass in umfangreichen wissenschaftlichen Experimenten 800 Kätzchen mit brauner und schwarzer Fellfarbe darauf untersucht wurden, ob diese in friedlicher Koexistenz mit Vasen leben können. Dabei wurde herausgefunden, dass 19,6% all dieser Katzen offenbar die Vasen mit Mäusen verwechseln, was zu einer erheblichen Verringerung der „Lebenserwartung” besagter Vasen führt. Bei genauerer Beobachtung wurde ermittelt, dass die braun gefärbten Katzen eine besondere Neigung zu diesem Verhalten zeigen. Insgesamt gelten unter ihnen 12,2% als Vasenumschmeißer. Wie hoch ist der Anteil der schwarzen Katzen, die keine Vasenumschmeißer sind? (Hinweis: Die Anzahl der braunen Katzen wird später noch gezählt (siehe unterhalb der zweiten Abbildung).)
Tragen wir zunächst die bekannten Werte ein. Es gibt das Merkmal „Fellfarbe” (schwarz, braun) und das Merkmal „Beziehung zu Vasen” (Vasenumschmeißer, Vasenliebhaber). Es gilt h800(Vasenumschmeißer) = 0,196 und h800(braun ∩ Vasenumschmeißer) = 0,122. Die Ausgangstabelle lautet demnach:
Da wir wissen, dass sich die Wahrscheinlichkeiten für den Wert, dass eine Katze eine Vasenumschmeißer-Katze ist zu 19,6% addieren und auf braune Katzen bereits 12,2% entfallen muss gelten:
h800(schwarz ∩ Vasenumschmeißer) = h800(Vasenumschmeißer) - h800(braun ∩ Vasenumschmeißer) = 0,196 - 0,122 = 0,074.
Es neigen also 7,4% der schwarzen Katzen zum Umschmeißen von Vasen. Wir wissen ferner, dass sich der Anteil der Vasenumschmeißer und der der Vasenliebhaber zu 100% bzw. 1 addieren muss. Es gilt also
h800(Vasenliebhaber) = 1 - h800(Vasenumschmeißer) = 1 - 0,196 = 0,756,
was 75,6% entspricht. Tragen wir diese Werte zunächst in die Tabelle ein:
Nun kommen wir nicht mehr recht weiter, da wir nichts über die Verteilungen der Fellfarben wissen. Einer der Wissenschaftler unterbicht daher seine Dauerkaffepause und kann nach kurzer Zeit berichten, dass 287 der 800 Katzen braun sind. Der Anteil der braunen Katzen liegt demnach bei (287/800) = 0,35875 bzw. 35,875%. Da wir wissen, dass h800(braun ∩ Vasenumschmeißer) = 0,122 gilt demnach
h800(braun ∩ Vasenliebhaber) = h800(braun) - h800(braun ∩ Vasenumschmeißer) = 0,35875 - 0,122 = 0,23675.
Da sich der Anteil der schwarzen und der braunen Katzen zu 100% bzw. 1 addiert wissen wir zudem, dass gilt
h800(schwarz) = 1 - h800(braun) = 1 - 0,35875 = 0,64125.
Nun können wir auch das letzte Feld, nämlich den Anteil der schwarzen Katzen, die Vasenliebhaber sind, errechnen:
h800(schwarz ∩ Vasenliebhaber) = h800(schwarz) - h800(schwarz ∩ Vasenumschmeißer) = 0,64125 - 0,074 = 0,56725.
Tragen wir nun die neuen Werte ein:
4. Quiz
Welcher der nachfolgenden Werte würde in einem der inneren Felder einer Vierfeldertafel für relative Häufigkeiten stehen?
hn(A ∪ B)
hn(A ∩ B)
hn(A)
hn(A) + hn(B) + 1
Zu welchen Wert können die rechten beiden Randsummen oder die unteren beiden Randsummen einer Vierfeldertafel für relative Häufigkeiten addiert werden?
0
1
2
100
Angenommen es wird eine Vierfeldertafel für relative Häufigkeiten aufgestellt. Für die Randsumme von 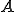 wurde der Wert 0,3 ermittelt. Wie lautet der Wert für die Randsumme von
wurde der Wert 0,3 ermittelt. Wie lautet der Wert für die Randsumme von 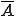 ?
?
0,3
0,7
1
Lässt sich aus diesen Werten nicht errechnen.
Angenommen es wird eine Vierfeldertafel für relative Häufigkeiten aufgestellt. Für die Randsumme von A wurde der Wert 0,2287 ermittelt. Wie lautet der Wert für die Randsumme von B?
1
0,7713
Lässt sich aus diesen Werten nicht errechnen.
0
Kommentare (4)
Von neu nach altWir bitten um ihr Verständnis.
ich find die Erklärungen auch ganz toll, die Fehler sind mir auch aufgefallen. Wäre gut wenn man die bald ausbessern könnte.
sonst alles gut erklärt!
Grüße
ich find die Erklärungen auch ganz toll, die Fehler sind mir auch aufgefallen. Wäre gut wenn man die bald ausbessern könnte.
sonst alles gut erklärt!
Grüße
ich glaube oben in der Schnellübersicht ist auch ein Fehler
"•Die Werte einer Spalte oder Reihe können aufsummiert werden, um die Randsumme zu erhalten. Es gilt beispielsweise (für die relative Häufigkeit): hn(A ∩ B) = hn(A ∩ B) + hn(A ∩ nicht B)"
Muss doch heißen hn(A) = hn(A ∩ B) + hn(A ∩ nicht B)"
es geht um das Beispiel mit den Katzen:
Die Berechnung der relativen Häufigkeit der Vasenliebhaber ist falsch (Bild 2).
h800(Vasenliebhaber) = 1 - h800(Vasenumschmeißer) = 1 - 0,196 = 0,756
ist nicht 0,756 sondern 0,804!
Sollte vielleicht mal ausgebessert werden und natürlich die Nachfolgefehler auch ;)
Ansonsten ist die Vorgehensweiße der Vierfeldertafel gut erklärt und auch anschaulich aufgemacht!
Mit freundlichen Grüßen,
Tay
FOS 12 Schüler