Stochastische Unabhängigkeit (Stochastik)

1. Definition

Zwei Ergeignisse A und B sind stochastisch unabhängig wenn gilt

$Formel-Code: P(A \cap B) = P(A) \cdot P(B)$

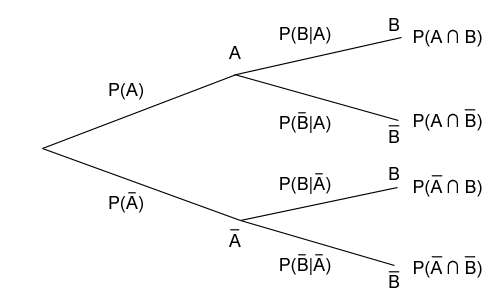
Anhand eines Baumdiagramms kann diese Formel nachvollzogen werden. Stellen wir uns ein mehrstufiges Zufallsexperiment vor bei dem erst A (oder nicht A) und dann B (oder nicht B) eintritt.

Die Wahrscheinlichkeit, dass nachdem A eingetreten ist auch B eintritt ist die bedingte Wahrscheinlichkeit P(B|A). Wenn nun P(B|A) identisch ist mit P(B) (also P(B|A) = P(B)), dann kann P(A ∩ B) durch multiplizieren von P(A) mit P(B) ermittelt werden, also P(A ∩ B) = P(A)P(B). Was heißt das, wenn P(B) = P(B|A) gilt? Das heißt, dass es keine Rolle für die Wahrscheinlichkeit von B spielt ob zuvor A eingetreten ist — die Wahrscheinlichkeiten beider Ereignisse sind daher unabhängig voneinander. Wenn sie jedoch abhängig voneinander sind, dann spielt es sehr wohl eine Rolle ob A vor B eingetreten ist oder stattdessen $Formel-Code: \overline{A}$ . Dann ist auch P(B|A) ungleich P(B) und die Wahrscheinlichkeit von P(A B) ergibt sich nicht mehr über P(A)*P(B).

2. Beispiel: Münzwurf

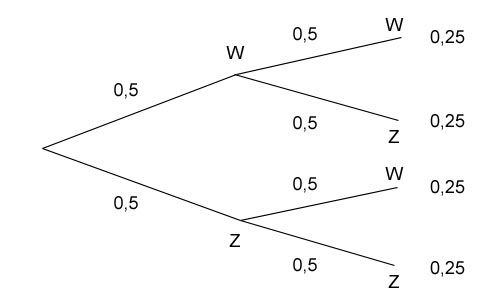
Als erstes Beispiel soll der Münzwurf dienen. Wir werfen die Münze zwei mal und können jeweils Wappen oder Zahl erhalten.

Baumdiagramm zum Münzwurf

Beim ersten Wurf genauso wie beim zweiten ist die Wahrscheinlichkeit für Wappen jeweils 50% bzw. 0,5. (Analog für Zahl ebenfalls 50% bzw. 0,5 bei beiden Würfen.) Entsprechend hat jeder mögliche Ausgang des mehrstufigen Zufallsexperiments ({Wappen, Wappen}, {Wappen, Zahl}, {Zahl, Wappen}, {Zahl, Zahl}) eine Wahrscheinlichkeit von 0,5*0,5=0,25.
Dementsprechend ist die Wahrscheinlichkeit für Wappen P(Wappen) beim zweiten Wurf identisch mit der bedingten Wahrscheinlichkeit P(Wappen|Zahl) (und auch P(Wappen|Wappen)). Es spielt also keine Rolle was die Münze beim ersten Wurf ergeben hat. Es liegt daher stochastische Unabhängigkeit vor, denn das Ergebnis des zweiten Wurfs ist vom ersten Wurf unabhängig. Dies bestätigt sich bei der Anwendung der Formel:

$Formel-Code: P(Zahl) \cdot P(Wappen) = 0,5 \cdot 0,5 = 0,25 = P(Zahl \cap Wappen)$

3. Beispiel: Urne

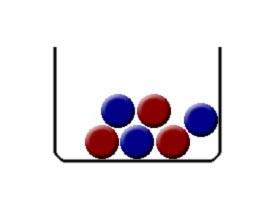
Stellen wir uns nun eine Urne vor in der 3 rote und 3 blaue Kugeln liegen.

Urne mit 3 roten und 3 blauen Kugeln

Wir ziehen per Zufall zwei mal aus der Urne, jeweils ohne die Kugel zurückzulegen. Die Ereignisse seien Er: rote Kugel gezogen und Eb: blaue Kugel gezogen. Wir wollen nun herausfinden, ob die Ereignisse Er und Eb stochastisch unabhängig sind.
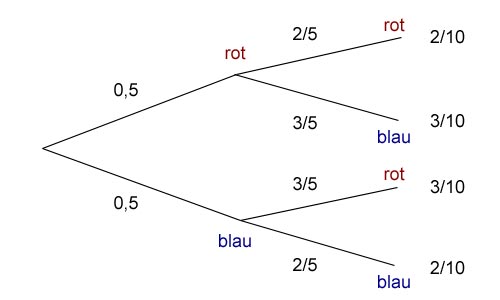
Zu Anfang sind 6 Kugeln im Gefäß, wovon 3 rot und 3 blau sind. Die Wahrscheinlichkeit, eine rote Kugel zu ziehen liegt demnach (wenn man zuvor nicht gezogen hat) bei $Formel-Code: \frac{3}{6}$ . Es gilt also P(Er) = 0,5. Genauso gilt für P(Eb) = 0,5.
Wurde im ersten Zug eine rote Kugel gezogen, dann gilt für den zweiten Zug $Formel-Code: P(E_b|E_r) = \frac{3}{5}$ , denn es sind noch 5 Kugeln übrig von denen 3 blau und 2 rot sind. Die beschriebenen und alle weiteren Wahrscheinlichkeiten sind im nachfolgenden Diagramm eingetragen.

Baumdiagramm zur Urne.
Erster Zug: 3 rote, 3 blaue Kugeln
Zweiter Zug: 2 rote, 3 blaue Kugeln oder 3 rote und 2 blaue Kugeln

Die Wahrscheinlichkeit, dass sowohl Er als auch Eb eintreten berechnet sich nun wie folgt:

$Formel-Code: P(E_r \cap E_b) = P(E_r) \cdot P(E_b|E_r) = \frac{3}{6} \cdot \frac{3}{5} = \frac{9}{30} = \frac{3}{10} = 0,3$

Wir berechnen nun P(Er)*P(Eb):

$Formel-Code: P(E_r) \cdot P(E_b) = \frac{3}{6} \cdot \frac{3}{6} = \frac{9}{36} = \frac{1}{4} = 0,25$

Demnach gilt, dass P(Er ∩ Eb) ≠ P(Er)*P(Eb), denn 0,4 ≠ 0,25. Die beiden Ereignisse sind also stochastisch abhängig (denn die Wahrscheinlichkeit, dass man eine blaue Kugel zieht ist abhängig davon welche Kugel zuvor gezogen wurde).

4. Beispiel: Würfelwurf

Bisher wurde die stochastische Unabhängigkeit an mehrstufigen Zufallsexperimenten vorgeführt. Es können aber auch zwei Ereignisse bei einem Zufallsexperiment mit nur einem Vorgang stochastisch abhängig voneinander sein. Stellen wir uns dazu den Würfelwurf vor.

Definieren wir nun die Ereignisse Egerade={2, 4, 6} und Eungerade={1, 3, 5}. Es lassen sich folgende Wahrscheinlichkeiten ermitteln:

$Formel-Code: P(E_{gerade}) = \frac{3}{6} = 0,5$
$Formel-Code: P(E_{ungerade}) = \frac{3}{6} = 0,5$
$Formel-Code: P(E_{gerade} \cap E_{ungerade}) = P(\empty) = 0$

Daher gilt $Formel-Code: P(E_{gerade} \cap E_{ungerade}) \not{=} P(E_{gerade}) \cdot P(E_{ungerade})$ , denn 0 ≠ 0,5*0,5. Die beiden Ereignisse sind also stochastisch abhängig. Wenn man eine gerade Augenzahl gewürfelt hat, denn kann man nicht gleichzeitig auch eine ungerade Augenzahl würfeln und umgekehrt.

Definieren wir wiederum die Ereignisse E1 = {1, 2} und E2 = {2, 3}, dann gilt:

$Formel-Code: P(E_{1}) = \frac{2}{6}$
$Formel-Code: P(E_{2}) = \frac{2}{6}$
$Formel-Code: P(E_{1} \cap E_{2}) = P(\{2\}) = \frac{1}{6}$

Es gilt wieder $Formel-Code: P(E_{1} \cap E_{2}) \not{=} P(E_{1}) \cdot P(E_{2})$ und die beiden Ereignisse sind stochastisch abhängig. Auch Ereignisse, die einige Elementarereignisse gemeinsam haben müssen nicht zwangsweise stochastisch unabhängig sein.

5. Stochastische Unabhängigkeit und Vierfeldertafel

Auf stochastische Unabhängigkeit kann logischerweise in vielen Fällen über eine Vierfeldertafel geprüft werden. Unten ist eine beispielhaft ausgefüllte Tabelle zu sehen.

		$Formel-Code: \overline{A}$	Summe
	0,1	0,2	0,3
$Formel-Code: \overline{B}$	0,4	0,3	0,7
Summe	0,5	0,5	1

Für A und B gelten demnach die Wahrscheinlichkeiten

P(A) = 0,5 (unten links, Randsumme der Spalte A)
P(B) = 0,3 (oben rechts, Randsumme der Reihe B)
P(A ∩ B) = 0,1 (Feld in dem sich die Spalte A und die Reihe B schneiden)

Da nun gilt P(A ∩ B) ≠ P(A)*P(B) sind hier die Ereignisse A und B stochastisch abhängig.

6. Stochastische Unabhängigkeit von 3 Ereignissen

Der Vollständigkeit halber sei noch die Bestimmung der stochastischen Unabhängigkeit für drei Ereignisse A, B und C erläutert. Diese ist sehr ähnlich zum Fall mit zwei Ereignissen. Es wird jede mögliche Schnittmenge zwischen den Ereignissen gebildet und die Wahrscheinlichkeit jeweils mit den ausmultiplizierten Wahrscheinlichkeiten verglichen:

P(A ∩ B) = P(A)*P(B)
P(A ∩ C) = P(A)*P(C)
P(B ∩ C) = P(B)*P(C)
P(A ∩ B ∩ C) = P(A)*P(B)*P(C)

Alle vier obenstehenden Punkte müssen erfüllt sein damit die drei Ereignisse stochastisch unabhängig sind.

7. Quiz

Zwei Ereignisse gelten als stochastisch unabhängig wenn gilt...?

P(A ∪ B) = P(A)*P(B)

P(A) = P(A ∩ B)*P(B)

P(A ∩ B) = P(A)*P(B)

P(A ∩ B) = P(B)*P(B|A)

#6999

8. Links

Kommentare (4)

Von neu nach alt

Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.

Danke

Beide Fehler korrigiert.

Der Baum bei der Definition ist falsch, oder?
Der Strang nach P(A-nicht) muss P(B|A nicht) sein und nicht P(B-nicht|A-nicht)

Da nun gilt P(A ∩ B) ≠ P(A)*P(B) sind hier die Ereignisse A und B stochastisch unabhängig.

richtig wäre: A und B sind stochastisch abhängig ;)

Stochastische Unabhängigkeit (Thema: Stochastik)

Erklärung des Begriffs "stochastische Unabhängigkeit", inklusive Definition, Beispiele und Anwendung auf Vierfeldertafel