Schnellübersicht
Zuvor wurde erläutert, dass die Laplace-Formel nur dann angewendet werden kann, wenn alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben (wie z. B. beim Würfelwurf). Was macht man nun, wenn dies nicht der Fall ist? Dann helfen einem die absolute und relative Häufigkeit weiter. Das Prinzip dabei ist denkbar simpel: das Zufallsexperiment wird schlicht möglichst oft durchgeführt und am Ende berechnet man die Wahrscheinlichkeiten einzelner Elementarereignisse aus den gesammelten Daten. Anders ausgedrückt: statt die Wahrscheinlichkeit theoretisch herzuleiten wird sie auf praktischem Weg ermittelt.
Die absolute Häufigkeit kann auch schlicht als Anzahl bezeichnet werden. Sie gibt wider, wie häufig ein Ereignis bei der Durchführung eines Zufallsexperiments (nach beliebig vielen Wiederholungen) eingetreten ist. Sie wird mathematisch mit H abgekürzt.
Beispiel: Angenommen man befragt per Zufall 1000 Personen nach ihrer Religion. Definieren wir nun für die Antwort das Ereignis E={Jedi}. Wenn nun 42 Personen gesagt haben, dass sie Jedi sind, dann gilt H(E) = 42 (und entsprechend H(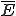
)=958).
Während die absolute Häufigkeit die Anzahl widergibt, beschreibt die relative Häufigkeit den Anteil eines Ereignisses. Die mathematische Schreibweise für die relative Häufigkeit ist hn, wobei n die Anzahl der Wiederholungen des Zufallsexperiments ist (im vorherigen Beispiel zur absoluten Häufigkeit wären das z. B. 1000 gewesen).
Soll die relative Häufigkeit eines Ereignisses E für ein Zufallsexperiment geprüft werden und werden n Wiederholungen dieses Experiments durchgeführt, dann ergibt sich die relative Häufigkeit aus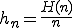
(H(n) ist die absolute Häufigkeit).
Beispiel: Angenommen das Amt für Verkehrssicherheit und Fahrfreude will testen, welche Auswirkungen technische Defekte auf das Fahrverhalten haben. Es lässt daher zur Hauptverkehrszeit die Ampeln einer großen Kreuzungen auf allen Seiten auf grün schalten und zählt die anschließenden Unfälle mit Totalschaden (E={Totalschaden}). Nach 750 Autos, die versucht haben die Kreuzung zu passieren, wurden insgesamt 46 Unfälle mit 3 Totalschäden registriert. Daher gilt für die absolute Häufigkeit H(E)=3. Die relative Häufigkeit lautet nun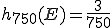
(0,004).
Wie zuvor erläutert, lautet die Laplace-Formel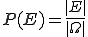
, was auch mit
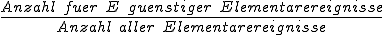umschrieben wird. Die relative Häufigkeit kann wiederum mit
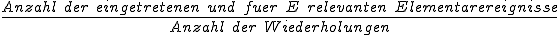umschrieben werden. Die beiden Formeln besitzen also eine recht hohe Ähnlichkeit. Diese Ähnlichkeit spiegelt sich auch in den Namen wider: während die Laplace-Formel als die „klassiche Definition der Wahrscheinlichkeit” bezeichnet wird, nennt man die relative Häufigkeit die „statistische Definition der Wahrscheinlichkeit”.
Die umgangssprachlichen Begriffe Anzahl und Anteil sind vermutlich einfacher zu merken als die Formeln. Beide beginnen mit „An”, sodass man sie zu AnnA verknüpfen kann. Übrigens lassen sich fast alle Buchstaben von „Anteil” in „relative” wiederfinden (nur das n fehlt), was die Zuordnung etwas vereinfacht.
Anzahl: Absolute Häufigkeit
Anteil: Relative Häufigkeit
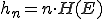
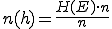
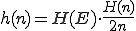
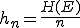
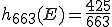
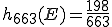
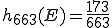
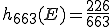
- Absolute und relative Häufigkeit werden aus den Ergebnissen eines Zufallsexperiments abgeleitet (nach beliebig vielen Wiederholungen).
- Absolute Häufigkeit eines Ereignisses (H(E)): Gibt an, wie oft das Ereignis E nach n Wiederholungen eingetreten ist (=Anzahl).
- Relative Häufigkeit eines Ereignisses (hn(E)):
(=Anteil).
1. Einleitung
Zuvor wurde erläutert, dass die Laplace-Formel nur dann angewendet werden kann, wenn alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben (wie z. B. beim Würfelwurf). Was macht man nun, wenn dies nicht der Fall ist? Dann helfen einem die absolute und relative Häufigkeit weiter. Das Prinzip dabei ist denkbar simpel: das Zufallsexperiment wird schlicht möglichst oft durchgeführt und am Ende berechnet man die Wahrscheinlichkeiten einzelner Elementarereignisse aus den gesammelten Daten. Anders ausgedrückt: statt die Wahrscheinlichkeit theoretisch herzuleiten wird sie auf praktischem Weg ermittelt.
2. Absolute Häufigkeit
Die absolute Häufigkeit kann auch schlicht als Anzahl bezeichnet werden. Sie gibt wider, wie häufig ein Ereignis bei der Durchführung eines Zufallsexperiments (nach beliebig vielen Wiederholungen) eingetreten ist. Sie wird mathematisch mit H abgekürzt.
Beispiel: Angenommen man befragt per Zufall 1000 Personen nach ihrer Religion. Definieren wir nun für die Antwort das Ereignis E={Jedi}. Wenn nun 42 Personen gesagt haben, dass sie Jedi sind, dann gilt H(E) = 42 (und entsprechend H(
3. Relative Häufigkeit
Während die absolute Häufigkeit die Anzahl widergibt, beschreibt die relative Häufigkeit den Anteil eines Ereignisses. Die mathematische Schreibweise für die relative Häufigkeit ist hn, wobei n die Anzahl der Wiederholungen des Zufallsexperiments ist (im vorherigen Beispiel zur absoluten Häufigkeit wären das z. B. 1000 gewesen).
Soll die relative Häufigkeit eines Ereignisses E für ein Zufallsexperiment geprüft werden und werden n Wiederholungen dieses Experiments durchgeführt, dann ergibt sich die relative Häufigkeit aus
Beispiel: Angenommen das Amt für Verkehrssicherheit und Fahrfreude will testen, welche Auswirkungen technische Defekte auf das Fahrverhalten haben. Es lässt daher zur Hauptverkehrszeit die Ampeln einer großen Kreuzungen auf allen Seiten auf grün schalten und zählt die anschließenden Unfälle mit Totalschaden (E={Totalschaden}). Nach 750 Autos, die versucht haben die Kreuzung zu passieren, wurden insgesamt 46 Unfälle mit 3 Totalschäden registriert. Daher gilt für die absolute Häufigkeit H(E)=3. Die relative Häufigkeit lautet nun
4. Ähnlichkeiten zur Laplace-Formel
Wie zuvor erläutert, lautet die Laplace-Formel
5. Eselsbrücke
Die umgangssprachlichen Begriffe Anzahl und Anteil sind vermutlich einfacher zu merken als die Formeln. Beide beginnen mit „An”, sodass man sie zu AnnA verknüpfen kann. Übrigens lassen sich fast alle Buchstaben von „Anteil” in „relative” wiederfinden (nur das n fehlt), was die Zuordnung etwas vereinfacht.
Anzahl: Absolute Häufigkeit
Anteil: Relative Häufigkeit
6. Quiz
Welcher der folgenden Begriffe beschreibt am ehesten die absolute Häufigkeit?
Absolution
Verteilung
Anzahl
Menge
Welcher der folgenden Begriffe beschreibt am ehesten die relative Häufigkeit?
Abbildung
Substrat
Exponat
Anteil
Wie lautet die Formel für die relative Häufigkeit? (gegeben: Ereignis E, absolute Häufigkeit H, Anzahl der Wiederholungen n)
Angenommen 663 Personen werden darauf befragt, welche Sportarten sie treiben. Es geben (unter anderem) 173 Personen an, Fußball zu spielen, 125 zu joggen, 74 zu schwimmen und 53 spielen Basketball. Wie hoch ist die relative Häufigkeit von E wenn das Ereignis alle Teamsportarten umfasst?
Kommentare (5)
Von neu nach altWir bitten um ihr Verständnis.
man sollte für diejenigen die mit mathe nicht so viel anfangen können und vllt eifach hinnehmen was sie lesen, bei "Relative häufigkei" ein "=" zwischen "3/750" und "(0,004)" setzen um nicht zu verwirren (es könnte als multiflikation aufgefasst und gemerkt werden...
DANKE AN DIE ERSTELLER! super Seite, hilft auch mir, ein tag vor meiner Mathe-Lk-Abi-Klausur ^^