Schnellübersicht
Bisher wurden immer nur die Wahrscheinlichkeiten von einzelnen Ereignissen berechnet (z. B. P(E)). Es gibt aber durchaus auch Möglichkeiten zur Ermittlung komplexerer Wahrscheinlichkeiten, etwa P(A oder B), P(A und gleichzeitig B), P(A und nicht B). Zum Verständnis der Rechenweisen wird allerdings etwas mehr Mengentheorie benötigt als bisher. In diesem Artikel werden daher kurz die Vereinigungsmenge und die Schnittmenge vorgestellt. Zudem auch die Venn-Diagramme, die zur Skizzierung von Mengen dienen.
Angenommen es liegen zwei Mengen A und B vor. Beide enthalten jeweils n Elemente (mit a und b gekennzeichnet): A={a1, a2, ..., an}, B={b1, b2, ..., bn}.
Die Schnittmenge (mathematisches Symbol: ∩) stellt nun alle Elemente dar, die sowohl in A als auch in B enthalten sind: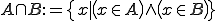
(Übersetzung: Jedes Element x, das ein Element in A und in B ist, ist auch ein Element der Schnittmenge).
Beispiel 1: Stellen wir uns zum Würfelwurf zwei Ereignisse vor mit E3;4={3, 4} und E4;5={4, 5}. Das erste Ereignis tritt also ein, wenn eine 3 oder eine 4 gewürfelt wird, das zweite hingegen bei einer 4 oder einer 5. Die Schnittmenge beider Ereignisse sind nun alle Elemente, die sowohl in E3;4 als auch in E4;5 enthalten sind. Die Rechnung lautet: E3;4 ∩ E4;5 = {3, 4} ∩ {4, 5} = {4}.
Beispiel 2: Angenommen wir definieren für den Würfelwurf Esicher=Ω={1, 2, 3, 4, 5, 6} und E≥4={4, 5, 6}. Die Schnittmenge lautet nun Esicher ∩ E≥4 = {1, 2, 3, 4, 5, 6} ∩ {4, 5, 6} = {4, 5, 6}.
Beispiel 3: Angenommen für den Münzwurf gelten die zwei Ereignisse EW={Wappen} und EZ={Zahl}. Die Schnittmenge lautete nun EW ∩ EZ = {Wappen} ∩ {Zahl} = ∅. Die Schnittmenge ist in diesem Fall also die leere Menge, da beide Mengen keine Gemeinsamkeiten haben.
Hinweis: Die Schnittmenge wird auch kurz als „Schnitt” bezeichnet. Für A ∩ B wird gesagt „A geschnitten B”. Es wird auch von einer logischen und-Verknüpfung gesprochen (alles was in A und in B ist). Man sagt dann: A und B.
Entsprechend ihrem Namen vereinigt die Vereinigungsmenge zwei Mengen miteinander. Ein Element muss daher nur in irgendeiner der beiden Mengen enthalten sein, um auch Teil der Vereinigungsmenge zu sein. Das mathematische Symbol für die Vereinigung ist ∪.
Beispiel 1: Nehmen wir wieder die beiden Ereignisse für den Münzwurf: EW={Wappen} und EZ={Zahl}. Für die Vereinigungsmenge gilt nun EW ∪ EZ = {Wappen} ∪ {Zahl} = {Wappen, Zahl}
Beispiel 2: Angenommen wir haben für einen Würfelwurf das Ereignis E1={1} und E6={6}, dann gilt für E1 ∪ E6 = {1} ∪ {6} = {1, 6}.
Beispiel 3: Angenommen für einen Würfelwurf werden die Ereignisse E≥3={3, 4, 5, 6} und E≥4={4, 5, 6} definiert, dann gilt für E≥3 ∪ E≥4 = {3, 4, 5, 6} ∪ {4, 5, 6} = {3, 4, 5, 6}
Hinweis: Die Vereinigungsmenge wird auch kurz als „Vereinigung” bezeichnet. Für A ∪ B wird gesagt „A vereinigt mit B”. Es wird auch von einer logischen oder-Verknüpfung gesprochen (alles was in A oder in B ist). Man sagt dann: A oder B.
Die leere Menge ist eine Menge, die keine Elemente enthält. Als Zeichen für die leere Menge wird entweder ∅ oder { } verwendet.
Beispiel: Für A={1, 2, 3} und B={4, 5, 6} ist die Schnittmenge die leere Menge, da A und B keine gemeinsamen Elemente enthalten. Es gilt also: A ∩ B = ∅.
Venn-Diagramme sind ein Mittel, um Mengen und die zuvor vorgestellten Operationen (Schnittmenge, Vereinigungsmenge) abzubilden und damit „greifbarer” zu machen. Die Mengen sind in den Abbildungen in Form von Flächen dargestellt, welche in einer übergeordneten Fläche (Ω, Ergebnisraum) liegen. Falls die dargestellten Mengen gleiche Elemente haben, überlappen sich auch die Flächen in den Abbildungen. Es folgen drei einfache Diagramme:
Wer nun Probleme damit hat, sich die Zeichen für die Vereinigungs- und die Schnittmenge zu merken (oder diese zuzordnen), dem könnte diese Eselsbrücke helfe: Das Zeichen für die Vereinigungsmenge (∪) stellt man sich als eine Art Tasse vor. In diese kann man verschiedene Mengen „gießen” und diese vermengen (bzw. „vereinigen”) sich in der Tasse — ohne, dass irgendetwas von den ursprünglichen Mengen verloren geht.
Das Zeichen für die Schnittmenge (∩) hingegen kann man als eine Art „Käseglocke” interpretieren. Diese stülpt man in der Mitte zwischen zwei Mengen über diese — was dann drunter passt bleibt auch drunter, der Rest der Mengen wird abgetrennt und geht verloren. Im Englischen spricht man auch von cup (Tasse) und cap (Haube).
Es gibt noch ein paar Gesetze im Bereich der Mengentheorie, die der Vollständigkeit halber erwähnt werden sollen. Die ersten beiden braucht man vielleicht mal beim Rechnen, die anderen beiden am ehesten für Beweise (falls man sie irgendwann mal anfertigen muss). Zu beachten ist: wenn man erstmal verstanden hat, was eine Vereinigungs- und was eine Schnittmenge ist, dann erschließen sich gerade die ersten beiden Gesetze von selbst und müssen nicht auswendig gelernt werden.
Gesetze für die Vereinigungsmenge:
Kommutativgesetz: A ∪ B = B ∪ A
Assoziativgesetz: (A ∪ B) ∪ C = A ∪ (B ∪ C)
Distributivgesetz: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
De-Morgang-Gesetze: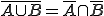
Die Gesetze für die Schnittmenge sind identisch (nur wird die Vereinigungsmenge durch die Schnittmenge ausgetauscht und umgekehrt).
- Schnittmenge: Die Schnittmenge (Zeichen: ∩) der Mengen A und B ist die Menge aller Elemente, die sowohl in A als auch in B enthalten sind.
- Vereinigungsmenge: Die Vereinigungsmenge (Zeichen: ∪) der Mengen A und B ist die Menge aller Elemente, die in A oder in B (oder in beiden) enthalten sind.
- Für A={2, 3} und B = {3, 4} gilt daher: A ∩ B = {3}, A ∪ B = {2, 3, 4}
- Eine leere Menge ist eine Menge, die leer ist, also keine Elemente enthält. Sie wird mit ∅ oder schlicht { } gekennzeichnet (z. B. A=∅ oder A={ }).
- Venn-Diagramme stellen Mengen und Beziehungen zwischen Mengen grafisch dar. Sie helfen dadurch beim Verständnis der Mengentheorie.
1. Einleitung
Bisher wurden immer nur die Wahrscheinlichkeiten von einzelnen Ereignissen berechnet (z. B. P(E)). Es gibt aber durchaus auch Möglichkeiten zur Ermittlung komplexerer Wahrscheinlichkeiten, etwa P(A oder B), P(A und gleichzeitig B), P(A und nicht B). Zum Verständnis der Rechenweisen wird allerdings etwas mehr Mengentheorie benötigt als bisher. In diesem Artikel werden daher kurz die Vereinigungsmenge und die Schnittmenge vorgestellt. Zudem auch die Venn-Diagramme, die zur Skizzierung von Mengen dienen.
2. Schnittmenge
Angenommen es liegen zwei Mengen A und B vor. Beide enthalten jeweils n Elemente (mit a und b gekennzeichnet): A={a1, a2, ..., an}, B={b1, b2, ..., bn}.
Die Schnittmenge (mathematisches Symbol: ∩) stellt nun alle Elemente dar, die sowohl in A als auch in B enthalten sind:
Beispiel 1: Stellen wir uns zum Würfelwurf zwei Ereignisse vor mit E3;4={3, 4} und E4;5={4, 5}. Das erste Ereignis tritt also ein, wenn eine 3 oder eine 4 gewürfelt wird, das zweite hingegen bei einer 4 oder einer 5. Die Schnittmenge beider Ereignisse sind nun alle Elemente, die sowohl in E3;4 als auch in E4;5 enthalten sind. Die Rechnung lautet: E3;4 ∩ E4;5 = {3, 4} ∩ {4, 5} = {4}.
Beispiel 2: Angenommen wir definieren für den Würfelwurf Esicher=Ω={1, 2, 3, 4, 5, 6} und E≥4={4, 5, 6}. Die Schnittmenge lautet nun Esicher ∩ E≥4 = {1, 2, 3, 4, 5, 6} ∩ {4, 5, 6} = {4, 5, 6}.
Beispiel 3: Angenommen für den Münzwurf gelten die zwei Ereignisse EW={Wappen} und EZ={Zahl}. Die Schnittmenge lautete nun EW ∩ EZ = {Wappen} ∩ {Zahl} = ∅. Die Schnittmenge ist in diesem Fall also die leere Menge, da beide Mengen keine Gemeinsamkeiten haben.
Hinweis: Die Schnittmenge wird auch kurz als „Schnitt” bezeichnet. Für A ∩ B wird gesagt „A geschnitten B”. Es wird auch von einer logischen und-Verknüpfung gesprochen (alles was in A und in B ist). Man sagt dann: A und B.
3. Vereinigungsmenge
Entsprechend ihrem Namen vereinigt die Vereinigungsmenge zwei Mengen miteinander. Ein Element muss daher nur in irgendeiner der beiden Mengen enthalten sein, um auch Teil der Vereinigungsmenge zu sein. Das mathematische Symbol für die Vereinigung ist ∪.
Beispiel 1: Nehmen wir wieder die beiden Ereignisse für den Münzwurf: EW={Wappen} und EZ={Zahl}. Für die Vereinigungsmenge gilt nun EW ∪ EZ = {Wappen} ∪ {Zahl} = {Wappen, Zahl}
Beispiel 2: Angenommen wir haben für einen Würfelwurf das Ereignis E1={1} und E6={6}, dann gilt für E1 ∪ E6 = {1} ∪ {6} = {1, 6}.
Beispiel 3: Angenommen für einen Würfelwurf werden die Ereignisse E≥3={3, 4, 5, 6} und E≥4={4, 5, 6} definiert, dann gilt für E≥3 ∪ E≥4 = {3, 4, 5, 6} ∪ {4, 5, 6} = {3, 4, 5, 6}
Hinweis: Die Vereinigungsmenge wird auch kurz als „Vereinigung” bezeichnet. Für A ∪ B wird gesagt „A vereinigt mit B”. Es wird auch von einer logischen oder-Verknüpfung gesprochen (alles was in A oder in B ist). Man sagt dann: A oder B.
4. Leere Menge
Die leere Menge ist eine Menge, die keine Elemente enthält. Als Zeichen für die leere Menge wird entweder ∅ oder { } verwendet.
Beispiel: Für A={1, 2, 3} und B={4, 5, 6} ist die Schnittmenge die leere Menge, da A und B keine gemeinsamen Elemente enthalten. Es gilt also: A ∩ B = ∅.
5. Venn-Diagramme
Venn-Diagramme sind ein Mittel, um Mengen und die zuvor vorgestellten Operationen (Schnittmenge, Vereinigungsmenge) abzubilden und damit „greifbarer” zu machen. Die Mengen sind in den Abbildungen in Form von Flächen dargestellt, welche in einer übergeordneten Fläche (Ω, Ergebnisraum) liegen. Falls die dargestellten Mengen gleiche Elemente haben, überlappen sich auch die Flächen in den Abbildungen. Es folgen drei einfache Diagramme:
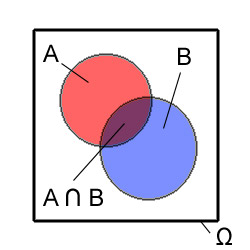
A ∩ B
Es sind die Mengen A und B in Form von Flächen innerhalb von Ω zu sehen. An dem Punkt, an dem sie sich überlappen liegen die gemeinsamen Elemente. Diese Elemente bilden die Schnittmenge.
Es sind die Mengen A und B in Form von Flächen innerhalb von Ω zu sehen. An dem Punkt, an dem sie sich überlappen liegen die gemeinsamen Elemente. Diese Elemente bilden die Schnittmenge.
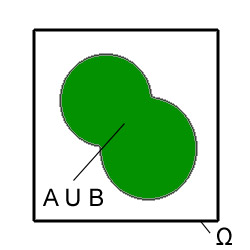
A ∪ B
Die neue Menge A ∪ B ersetzt in der Abbildung die alten Mengen A und B und enthält alle Elemente, die auch A und B enthalten haben (dargestellt durch die gleiche Fläche wie A und B).
Die neue Menge A ∪ B ersetzt in der Abbildung die alten Mengen A und B und enthält alle Elemente, die auch A und B enthalten haben (dargestellt durch die gleiche Fläche wie A und B).
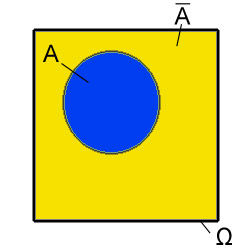
Zuletzt folgt noch ein kurzes Diagramm welches das Gegenereignis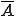 
zu A darstellt.
Wir erinnern uns: das Gegenereignis tritt immer dann ein, wenn A nicht eintritt.
Wir erinnern uns: das Gegenereignis tritt immer dann ein, wenn A nicht eintritt.
6. Eselsbrücke
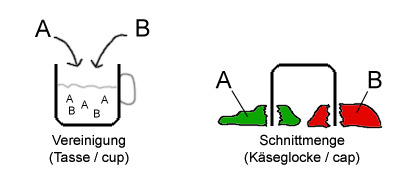
Wer nun Probleme damit hat, sich die Zeichen für die Vereinigungs- und die Schnittmenge zu merken (oder diese zuzordnen), dem könnte diese Eselsbrücke helfe: Das Zeichen für die Vereinigungsmenge (∪) stellt man sich als eine Art Tasse vor. In diese kann man verschiedene Mengen „gießen” und diese vermengen (bzw. „vereinigen”) sich in der Tasse — ohne, dass irgendetwas von den ursprünglichen Mengen verloren geht.
Das Zeichen für die Schnittmenge (∩) hingegen kann man als eine Art „Käseglocke” interpretieren. Diese stülpt man in der Mitte zwischen zwei Mengen über diese — was dann drunter passt bleibt auch drunter, der Rest der Mengen wird abgetrennt und geht verloren. Im Englischen spricht man auch von cup (Tasse) und cap (Haube).
7. Gesetze der Mengentheorie
Es gibt noch ein paar Gesetze im Bereich der Mengentheorie, die der Vollständigkeit halber erwähnt werden sollen. Die ersten beiden braucht man vielleicht mal beim Rechnen, die anderen beiden am ehesten für Beweise (falls man sie irgendwann mal anfertigen muss). Zu beachten ist: wenn man erstmal verstanden hat, was eine Vereinigungs- und was eine Schnittmenge ist, dann erschließen sich gerade die ersten beiden Gesetze von selbst und müssen nicht auswendig gelernt werden.
Gesetze für die Vereinigungsmenge:
Kommutativgesetz: A ∪ B = B ∪ A
Assoziativgesetz: (A ∪ B) ∪ C = A ∪ (B ∪ C)
Distributivgesetz: A ∪ (B ∩ C) = (A ∪ B) ∩ (A ∪ C)
De-Morgang-Gesetze:
Die Gesetze für die Schnittmenge sind identisch (nur wird die Vereinigungsmenge durch die Schnittmenge ausgetauscht und umgekehrt).
Gesetze für die Schnittmenge
Kommutativgesetz: A ∩ B = B ∩ A
Assoziativgesetz: (A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributivgesetz: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
De-Morgang-Gesetze: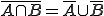
Assoziativgesetz: (A ∩ B) ∩ C = A ∩ (B ∩ C)
Distributivgesetz: A ∩ (B ∪ C) = (A ∩ B) ∪ (A ∩ C)
De-Morgang-Gesetze:
8. Quiz
Angenommen zwei Mengen A={173, 56, Z, 13, X} und B={Y, 0, 14, X} liegen vor. Wie lautet das Ergebnis von A ∩ B?
{173, 56, Z, 13}
{173, 56, Z, 13, X, Y, 0, 14}
{X}
{}
Angenommen zwei Mengen A={49, 50, 17, 23} und B={50, 17, 49, 23} liegen vor. Wie lautet das Ergebnis von A ∪ B?
{}
{49, 50, 17, 23, 50, 17, 49, 23}
{49, 50, 17, 23}
{49, 50, 23}
Angenommen zwei Mengen A={119, 2017, T-37, 42, 0-815, 95} und B=∅ liegen vor. Wie lautet das Ergebnis von A ∩ B?
{119, 2017, T-37, 42, 0-815, 95}
{119, 2017, T-37, 42, 0-815, 95, {}}
∅
{119, 2017, 42, 95}
Angenommen es liegen drei Mengen A={99, 100, 500}, B={500, 17}, C={99} liegen vor. Wie lautet das Ergebnis von (A ∪ B) ∩ C?
{ }
{99, 500}
{99}
{500}
Kommentare (3)
Von neu nach altWir bitten um ihr Verständnis.