Schnellübersicht
Angenommen es liegen n Elemente vor von denen k ausgewählt werden. Soll nun zu diesen k Elementen die Anzahl aller möglichen Anordnungen bestimmt werden, dann ergibt sich diese Anzahl über
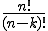 sofern jedes der k Elemente exakt ein mal verwendet wird („ohne Zurücklegen”).
sofern jedes der k Elemente exakt ein mal verwendet wird („ohne Zurücklegen”).
Die Variation mit Zurücklegen wird weiter unten erläutert.
Sonderform Permutation: Falls k identisch mit n ist (k=n), also alle verfügbaren Elemente ausgewählt werden sollen, dann wird dies häufig als Permutation bezeichnet. Da dann k=n ist und ferner gilt 0!=1 (die Fakultät von null ist 1) sieht die vereinfachte Formel für die Variation dann wie folgt aus:
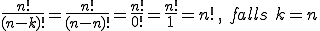
Angenommen der Zombie „Carl Friedrich Schmaus” hat bei einem Ausflug in einem Haus 6 leckere Menschen gefunden. Ein wahres Festessen! Natürlich überlegt er, wie er dieses Mahl wohl am besten genießen könnte. Während er darüber grübelt ob er erst Mensch A und dann C essen sollte oder vielleicht erst Mensch D und A und dann E und dann (... etc.) fragt er sich, in wie vielen verschiedenen Reihenfolgen er die Menschen wohl auffuttern könnte.
Lösung: Wenn davon ausgegangen wird, dass er alle sechs verspeist und nacheinander jeweils komplett (erst den ersten komplett, dann den zweiten komplett usw.), dann ist n=6, k=6 und wir haben einen Fall von „Ziehen ohne Zurücklegen”. Werden die Werte in die passende Formel eingesetzt dann ergibt sich:
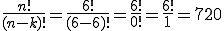 Carl Friedrich Schmaus kann die Menschen also in 720 verschiedenen Reihenfolgen essen. Seiner Kreativität sind kaum Grenzen gesetzt!
Carl Friedrich Schmaus kann die Menschen also in 720 verschiedenen Reihenfolgen essen. Seiner Kreativität sind kaum Grenzen gesetzt!
Nachdem Zombie Schmaus sich gerade seine Serviette umgebunden hat bemerkt er, wie draußen einer von diesen Gutmenschen mit einem Gewehr angelaufen kommt, die glauben, sie könnten die Welt durch die Ausrottung der armen Zombies verbessern. Sehr ärgerlich! Da Schmaus nur ungern die Reste seines verfaulten Gehirns an der Wand sehen will beschließt er, das Festmahl etwas kürzer zu halten. Er will nur noch 3 statt 6 Menschen verspeisen. Wie viele mögliche Anordnungen stehen ihm nun zur Verfügung?
Lösung: Die Formel bleibt die selbe, k ist aber nun gleich 3:
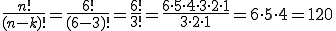 Es stehen Schmaus also noch 120 mögliche Reihenfolgen zur Verfügung.
Es stehen Schmaus also noch 120 mögliche Reihenfolgen zur Verfügung.
Wer von dem vielen Rechnen schon erschöpft ist, der darf jetzt aufatmen: die meisten modernen Taschenrechner haben eine Taste zum Ausrechnen des Bruchs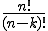 , sodass man nur noch das n und das k angeben muss, um das Ergebnis zu erhalten. Die Taste heißt zumeist nPr (ist nicht einheitlich zwischen den Marken). Das P steht für „Permutation”, da im Englischen die Variation als „Permutation” bezeichnet wird. (Die Taste ist nicht zu verwechseln mit nCr bei der das C für Combination bzw. Kombination steht und die im nächsten Artikel behandelt wird.) Die Eingabereihenfolge für nPr könnte dann für n=6 und k=3 lauten: 6, nPr, 3, =.
, sodass man nur noch das n und das k angeben muss, um das Ergebnis zu erhalten. Die Taste heißt zumeist nPr (ist nicht einheitlich zwischen den Marken). Das P steht für „Permutation”, da im Englischen die Variation als „Permutation” bezeichnet wird. (Die Taste ist nicht zu verwechseln mit nCr bei der das C für Combination bzw. Kombination steht und die im nächsten Artikel behandelt wird.) Die Eingabereihenfolge für nPr könnte dann für n=6 und k=3 lauten: 6, nPr, 3, =.
Bisher wurde gezogen ohne Zurücklegen. Das heißt, dass jedes der k Elemente in einer einzelnen möglichen Anordnung nur ein mal vorkommen durfte. Zieht man stattdessen mit Zurücklegen, dann dann darf jedes der k gezogenen Elemente mehrmals vorkommen (da es nach jedem Zug wieder zurückgelegt wird). Die Anzahl der verschiedenen Möglichkeiten k mal aus n Elementen zu ziehen ergibt sich dann über
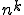
Angenommen die 120 möglichen Reihenfolgen sind Zombie Schmaus zu einschränkend. Er beschließt daher, jeden Menschen nur etwas anzuknabbern und ihn dann zurück zu den anderen zu legen. Danach kann er dann den nächsten auswählen, was ein bereits angeknabberter sein kann oder auch ein noch unberührter Mensch. Er könnte also beispielsweise B etwas anknabbern, zurücklegen, dann E anknabbern, zurücklegen, dann noch mal B anknabbern, zurücklegen und dann abhauen (er nimmt sich wieder nur 3 vor). Wie viele Reihenfolgen stehen ihm nun zur Verfügung?
Lösung: Es wird mit Zurücklegen gezogen. n ist gleich 6 und k gleich 3 (da sich die Werte seit dem letzten Beispiel nicht geändert haben). Die Rechnung lautet daher:
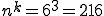 Nicht sehr viel mehr Anordnungen als vorher, aber Schmaus findet sich damit ab.
Nicht sehr viel mehr Anordnungen als vorher, aber Schmaus findet sich damit ab.
Würde er stattdessen 6 mal ziehen, dann würde das Ergebnis lauten:
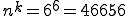
Je nachdem für welches k sich Zombie Schmaus entscheidet würde er folgende Ergebnisse erhalten (bei n=6):
Ziehen ohne Zurücklegen
Dass die Anzahl der Möglichkeiten von k=5 nach k=6 nicht mehr ansteigt hängt damit zusammen, dass nach Auswahl von 5 Elementen für das 6. Element nur noch eines zur Verfügung steht (bei n=6).
Ziehen mit Zurücklegen:
Beim Ziehen mit Zurücklegen gibt es hingegen eine hohe Steigerung auch bei k=6, da auch für den 6. Zug 6 Elemente zur Auswahl stehen (es wurde ja alle zuvor gewählten Elemente wieder zurückgelegt).
Nachdem bereits das Zombie-Beispiel vorgestellt wurden seien für die Variation beim Ziehen mit Zurücklegen noch zwei weitere Beispiele genannt, die recht beliebt sind.
Beispiel Toto: Das erste beliebte Beispiel ist das Fußball-Toto. Auf einem Wettschein stehen 11 Paarungen von Mannschaften. Für jede der Paarungen gibt man an, ob man glaubt, dass die erste Mannschaft gewinnt oder die zweite oder es zu einem Unentschieden kommt. Wie viele Möglichkeiten den Wettschein auszufüllen gibt es?
Lösung: Hierbei handelt es sich um eine Variation in der Form Ziehen mit Zurücklegen. Wir haben sozusagen eine Urne mit 3 Kugeln (Kugel 1: erstes Team gewinnt, Kugel 2: zweites Team gewinnt, Kugel 3: Unentschieden). Aus dieser Urne wird nun 11 mal gezogen und jedes mal die Kugel wieder zurückgelegt. Das besondere ist hier, dass das k größer als n ist. Beim Ziehen mit Zurücklegen darf das sein, dann die Urne wird nicht leer (man legt ja zurück). Beim Ziehen ohne Zurücklegen darf das k nie größer als n sein. Die Lösung lautet demnach:
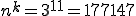 Man kann den Schein also auf 177.147 verschiedene Weisen ausfüllen.
Man kann den Schein also auf 177.147 verschiedene Weisen ausfüllen.
Beispiel Fahrradschloss: Angenommen wir haben ein Fahrradschloss mit 4 Rädern, deren Zahlen jeweils von 0 bis 9 reichen (also 10 verschiedene Zahlen). Nur wenn alle 4 Räder auf die richtige Zahl gestellt sind öffnet das Schloss. Um nun alle möglichen Anordnungen zu berechnen lautet das Vorgehen:
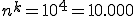 Nicht allzu schwer, da man es auch aus den Zahlen direkt ablesen kann (die Räder gehen bis 9999 und zusätzlich gibt es 0000, also 9999+1=10000). Nehmen wir stattdessen 5 Räder, die jeweils von 0 bis 7 reichen. Gibt es dann mehr Anordnungen?
Nicht allzu schwer, da man es auch aus den Zahlen direkt ablesen kann (die Räder gehen bis 9999 und zusätzlich gibt es 0000, also 9999+1=10000). Nehmen wir stattdessen 5 Räder, die jeweils von 0 bis 7 reichen. Gibt es dann mehr Anordnungen?
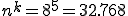 Fünf Räder mit jeweils 8 Zahlen sind also sicherer als 4 mit je 10 Zahlen.
Fünf Räder mit jeweils 8 Zahlen sind also sicherer als 4 mit je 10 Zahlen.
Spezialbeispiel Passwörter: Nicht beliebt, aber informativ ist das Beispiel, die Anzahl aller möglichen Passwörter für eine bestimmte Zeichenlänge zu zählen. Nehmen wir an, dass das Passwort exakt 8 Zeichen lang sein soll. Es sollen die Zeichen des Alphabets (26*2 Zeichen durch Groß- und Kleinschriebung) sowie die Zahlen von 0 bis 9 (10 Stück) verwendet werden. Wie viele Passwörter gibt es?
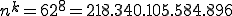 Knapp 218 Billionen Passwörter also. Ein Angreifer, der eine Million Passwörter pro Sekunde durchgeht würde knapp 218.340.105 Sekunden, also etwa 2527 Tage brauchen, um jedes denkbare Passwort durchzuprobieren. (In den meisten Fällen geht es allerdings viel schneller, da häufig Wörter verwendet, die auch in normalen Wörterbüchern stehen — und in so einem Wörterbuch stehen schließlich viel weniger als 218 Billionen Wörter drin.)
Knapp 218 Billionen Passwörter also. Ein Angreifer, der eine Million Passwörter pro Sekunde durchgeht würde knapp 218.340.105 Sekunden, also etwa 2527 Tage brauchen, um jedes denkbare Passwort durchzuprobieren. (In den meisten Fällen geht es allerdings viel schneller, da häufig Wörter verwendet, die auch in normalen Wörterbüchern stehen — und in so einem Wörterbuch stehen schließlich viel weniger als 218 Billionen Wörter drin.)
Die Herleitung des Ziehens mit Zurücklegen ([mimetetex]n^k[/mimetex]) ist eher einfach: Angenommen wir haben wieder n=6, dann stehen für den ersten Zug 6 Elemente zur Auswahl. Für den zweiten Zug wieder 6 (da das vorherige Element zurückgelegt wurde), für den dritten Zug ebenfalls 6 usw. Stellt man sich das ganze als Baum vor, dann gibt es bei jedem Zug 6 Abzweigungen. Mit jedem Zug steigt also die Gesamtzahl der möglichen Reihenfolge um das sechsfache an. Das wiederum ergibt die Formel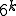 bzw. allgemeiner
bzw. allgemeiner 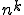 .
.
Die Herleitung des Ziehens ohne Zurücklegen ist etwas komplizierter. Am besten schaut man sich zuerst den Sonderfall der Permutation (n=k) an. Für diese lautet die vereinfachte Formel schlicht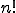 . Die Herleitung dieser Formel ist sehr vergleichbar zur vorherigen Herleitung der Variation für das Ziehen mit Zurücklegen. Angenommen wir starten wieder mit n=6 und wählen k=6. Beim ersten Zug haben wir dann 6 Auswahlmöglichkeiten. Da wir nicht zurücklegen schrumpft das n nach dem ersten Zug und wird zu 5. Für den zweiten Zug haben wir also nur noch 5 Auswahlmöglichkeiten. Für den dritten wiederum 5-1 also 4, usw. Die Gesamtzahl der Möglichkeiten ergibt sich demnach aus 6*5*4*3*2*1 und das ist identisch mit „6!”, was zur allgemeineren Formel
. Die Herleitung dieser Formel ist sehr vergleichbar zur vorherigen Herleitung der Variation für das Ziehen mit Zurücklegen. Angenommen wir starten wieder mit n=6 und wählen k=6. Beim ersten Zug haben wir dann 6 Auswahlmöglichkeiten. Da wir nicht zurücklegen schrumpft das n nach dem ersten Zug und wird zu 5. Für den zweiten Zug haben wir also nur noch 5 Auswahlmöglichkeiten. Für den dritten wiederum 5-1 also 4, usw. Die Gesamtzahl der Möglichkeiten ergibt sich demnach aus 6*5*4*3*2*1 und das ist identisch mit „6!”, was zur allgemeineren Formel 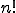 führt.
führt.
Was ist nun anders wenn k kleiner als n ist (k<n)? Vom Prinzip her eigentlich nichts, auch wenn die Formel anders aussieht. Wählen wir k=3 (mit n wieder 6), dann haben wir beim ersten Zug 6 Auswahlmöglichkeiten, beim zweiten Zug 5 und beim dritten Zug 4. Die Gesamtzahl der Möglichkeiten ergibt sich demnach aus 6*5*4 und ist demnach 120.
Nun kann man die berechtigte Frage stellen wieso die am Anfang genannte Formel anders aussieht (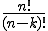 )? Das liegt daran, dass es schnell sehr aufwendig werden kann n*(n-1)*(n-2)*(n-3)*....*1 zu rechnen, etwa wenn man n=40 und k=35 wählt: dann müsste man 35 Werte miteinander multiplizieren! Daher versucht man es stattdessen auf die Fakultät zu bekommen für die es eine Taste auf (fast) jedem Taschenrechner gibt. Man errechnet daher die Fakultät von n (n!) schreibt diese in den Zähler eines Bruchs und kürzt über den Nenner einfach alles weg was „zu viel” ist. Gehen wir wieder vom Beispiel n=6 und k=3 aus, dann lautet das ganze:
)? Das liegt daran, dass es schnell sehr aufwendig werden kann n*(n-1)*(n-2)*(n-3)*....*1 zu rechnen, etwa wenn man n=40 und k=35 wählt: dann müsste man 35 Werte miteinander multiplizieren! Daher versucht man es stattdessen auf die Fakultät zu bekommen für die es eine Taste auf (fast) jedem Taschenrechner gibt. Man errechnet daher die Fakultät von n (n!) schreibt diese in den Zähler eines Bruchs und kürzt über den Nenner einfach alles weg was „zu viel” ist. Gehen wir wieder vom Beispiel n=6 und k=3 aus, dann lautet das ganze:
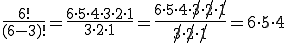 womit wir wieder bei der weiter oben genannten Rechenweise wären. Eine Variation ohne Zurücklegen mit n=6 und k=3 lässt sich also über 6*5*4 oder über
womit wir wieder bei der weiter oben genannten Rechenweise wären. Eine Variation ohne Zurücklegen mit n=6 und k=3 lässt sich also über 6*5*4 oder über 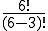 berechnen — beide Rechnungen sind letztlich gleich.
berechnen — beide Rechnungen sind letztlich gleich.

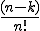
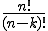
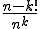
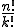


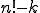
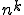
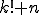
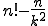
- Werden aus n Elementen nacheinander k gezogen und soll die Anzahl aller möglichen verschiedenen Anordnungen dieser k Elemente gezählt werden, dann wird von einer Variation gesprochen.
- Die Formel für die Variation ohne Zurücklegen mit n Elementen von denen k gezogen werden lautet
. Der Spezialfall k=n wird als Permutation bezeichnet. Die Formel kann dann zu n! vereinfacht werden (ergibt sich durch Einsetzen, da gilt 0!=1).
- Die Formel für die Variation mit Zurücklegen lautet
(bei n Elementen von denen k gezogen werden).
1. Einleitung
Angenommen es liegen n Elemente vor von denen k ausgewählt werden. Soll nun zu diesen k Elementen die Anzahl aller möglichen Anordnungen bestimmt werden, dann ergibt sich diese Anzahl über
Die Variation mit Zurücklegen wird weiter unten erläutert.
Sonderform Permutation: Falls k identisch mit n ist (k=n), also alle verfügbaren Elemente ausgewählt werden sollen, dann wird dies häufig als Permutation bezeichnet. Da dann k=n ist und ferner gilt 0!=1 (die Fakultät von null ist 1) sieht die vereinfachte Formel für die Variation dann wie folgt aus:
2. Beispiel zur Variation ohne Zurücklegen mit k=n
Angenommen der Zombie „Carl Friedrich Schmaus” hat bei einem Ausflug in einem Haus 6 leckere Menschen gefunden. Ein wahres Festessen! Natürlich überlegt er, wie er dieses Mahl wohl am besten genießen könnte. Während er darüber grübelt ob er erst Mensch A und dann C essen sollte oder vielleicht erst Mensch D und A und dann E und dann (... etc.) fragt er sich, in wie vielen verschiedenen Reihenfolgen er die Menschen wohl auffuttern könnte.
Lösung: Wenn davon ausgegangen wird, dass er alle sechs verspeist und nacheinander jeweils komplett (erst den ersten komplett, dann den zweiten komplett usw.), dann ist n=6, k=6 und wir haben einen Fall von „Ziehen ohne Zurücklegen”. Werden die Werte in die passende Formel eingesetzt dann ergibt sich:
3. Beispiel zur Variation ohne Zurücklegen mit k≠n
Nachdem Zombie Schmaus sich gerade seine Serviette umgebunden hat bemerkt er, wie draußen einer von diesen Gutmenschen mit einem Gewehr angelaufen kommt, die glauben, sie könnten die Welt durch die Ausrottung der armen Zombies verbessern. Sehr ärgerlich! Da Schmaus nur ungern die Reste seines verfaulten Gehirns an der Wand sehen will beschließt er, das Festmahl etwas kürzer zu halten. Er will nur noch 3 statt 6 Menschen verspeisen. Wie viele mögliche Anordnungen stehen ihm nun zur Verfügung?
Lösung: Die Formel bleibt die selbe, k ist aber nun gleich 3:
4. Variation ohne Zurücklegen per Taschenrechner
Wer von dem vielen Rechnen schon erschöpft ist, der darf jetzt aufatmen: die meisten modernen Taschenrechner haben eine Taste zum Ausrechnen des Bruchs
5. Variation bei Ziehen mit Zurücklegen
Bisher wurde gezogen ohne Zurücklegen. Das heißt, dass jedes der k Elemente in einer einzelnen möglichen Anordnung nur ein mal vorkommen durfte. Zieht man stattdessen mit Zurücklegen, dann dann darf jedes der k gezogenen Elemente mehrmals vorkommen (da es nach jedem Zug wieder zurückgelegt wird). Die Anzahl der verschiedenen Möglichkeiten k mal aus n Elementen zu ziehen ergibt sich dann über
6. Beispiel zur Variation mit Zurücklegen
Angenommen die 120 möglichen Reihenfolgen sind Zombie Schmaus zu einschränkend. Er beschließt daher, jeden Menschen nur etwas anzuknabbern und ihn dann zurück zu den anderen zu legen. Danach kann er dann den nächsten auswählen, was ein bereits angeknabberter sein kann oder auch ein noch unberührter Mensch. Er könnte also beispielsweise B etwas anknabbern, zurücklegen, dann E anknabbern, zurücklegen, dann noch mal B anknabbern, zurücklegen und dann abhauen (er nimmt sich wieder nur 3 vor). Wie viele Reihenfolgen stehen ihm nun zur Verfügung?
Lösung: Es wird mit Zurücklegen gezogen. n ist gleich 6 und k gleich 3 (da sich die Werte seit dem letzten Beispiel nicht geändert haben). Die Rechnung lautet daher:
Würde er stattdessen 6 mal ziehen, dann würde das Ergebnis lauten:
7. Alle Ergebnisse zum Zombie-Beispiel
Je nachdem für welches k sich Zombie Schmaus entscheidet würde er folgende Ergebnisse erhalten (bei n=6):
Ziehen ohne Zurücklegen
| k | Mögliche verschiedene Anordnungen |
| 1 | 6 |
| 2 | 30 |
| 3 | 120 |
| 4 | 360 |
| 5 | 720 |
| 6 | 720 |
Ziehen mit Zurücklegen:
| k | Mögliche verschiedene Anordnungen |
| 1 | 6 |
| 2 | 36 |
| 3 | 216 |
| 4 | 1296 |
| 5 | 7776 |
| 6 | 46656 |
8. Weitere Beispiele zur Variation bei Ziehen mit Zurücklegen
Nachdem bereits das Zombie-Beispiel vorgestellt wurden seien für die Variation beim Ziehen mit Zurücklegen noch zwei weitere Beispiele genannt, die recht beliebt sind.
Beispiel Toto: Das erste beliebte Beispiel ist das Fußball-Toto. Auf einem Wettschein stehen 11 Paarungen von Mannschaften. Für jede der Paarungen gibt man an, ob man glaubt, dass die erste Mannschaft gewinnt oder die zweite oder es zu einem Unentschieden kommt. Wie viele Möglichkeiten den Wettschein auszufüllen gibt es?
Lösung: Hierbei handelt es sich um eine Variation in der Form Ziehen mit Zurücklegen. Wir haben sozusagen eine Urne mit 3 Kugeln (Kugel 1: erstes Team gewinnt, Kugel 2: zweites Team gewinnt, Kugel 3: Unentschieden). Aus dieser Urne wird nun 11 mal gezogen und jedes mal die Kugel wieder zurückgelegt. Das besondere ist hier, dass das k größer als n ist. Beim Ziehen mit Zurücklegen darf das sein, dann die Urne wird nicht leer (man legt ja zurück). Beim Ziehen ohne Zurücklegen darf das k nie größer als n sein. Die Lösung lautet demnach:
Beispiel Fahrradschloss: Angenommen wir haben ein Fahrradschloss mit 4 Rädern, deren Zahlen jeweils von 0 bis 9 reichen (also 10 verschiedene Zahlen). Nur wenn alle 4 Räder auf die richtige Zahl gestellt sind öffnet das Schloss. Um nun alle möglichen Anordnungen zu berechnen lautet das Vorgehen:
Spezialbeispiel Passwörter: Nicht beliebt, aber informativ ist das Beispiel, die Anzahl aller möglichen Passwörter für eine bestimmte Zeichenlänge zu zählen. Nehmen wir an, dass das Passwort exakt 8 Zeichen lang sein soll. Es sollen die Zeichen des Alphabets (26*2 Zeichen durch Groß- und Kleinschriebung) sowie die Zahlen von 0 bis 9 (10 Stück) verwendet werden. Wie viele Passwörter gibt es?
9. Herleitung
Die Herleitung des Ziehens mit Zurücklegen ([mimetetex]n^k[/mimetex]) ist eher einfach: Angenommen wir haben wieder n=6, dann stehen für den ersten Zug 6 Elemente zur Auswahl. Für den zweiten Zug wieder 6 (da das vorherige Element zurückgelegt wurde), für den dritten Zug ebenfalls 6 usw. Stellt man sich das ganze als Baum vor, dann gibt es bei jedem Zug 6 Abzweigungen. Mit jedem Zug steigt also die Gesamtzahl der möglichen Reihenfolge um das sechsfache an. Das wiederum ergibt die Formel
Die Herleitung des Ziehens ohne Zurücklegen ist etwas komplizierter. Am besten schaut man sich zuerst den Sonderfall der Permutation (n=k) an. Für diese lautet die vereinfachte Formel schlicht
Was ist nun anders wenn k kleiner als n ist (k<n)? Vom Prinzip her eigentlich nichts, auch wenn die Formel anders aussieht. Wählen wir k=3 (mit n wieder 6), dann haben wir beim ersten Zug 6 Auswahlmöglichkeiten, beim zweiten Zug 5 und beim dritten Zug 4. Die Gesamtzahl der Möglichkeiten ergibt sich demnach aus 6*5*4 und ist demnach 120.
Nun kann man die berechtigte Frage stellen wieso die am Anfang genannte Formel anders aussieht (
10. Quiz
Wie lautet die normale Formel für die Variation ohne Zurücklegen bei n Elementen von denen k ausgewählt werden?
Wie wird die Variation ohne Zurücklegen bezeichnet wenn k=n ist?
Permutation
Normalisation
Pseudovariation
Kanalisation
Wie lautet die Formel für die Variation mit Zurücklegen bei n Elementen, wenn k mal gezogen wird?
Kommentare (5)
Von neu nach altWir bitten um ihr Verständnis.
Der Fehler bei der Berechnung der möglichen Passwörter ist jetzt korrigiert.
Spezialbeispiel Passwörter: Nicht beliebt, aber informativ ist das Beispiel, die Anzahl aller möglichen Passwörter für eine bestimmte Zeichenlänge zu zählen. Nehmen wir an, dass das Passwort exakt 8 Zeichen lang sein soll. Es sollen die Zeichen des Alphabets (26*2 Zeichen durch Groß- und Kleinschriebung) sowie die Zahlen von 0 bis 9 (10 Stück) verwendet werden. Wie viele Passwörter gibt es?
Formel-Code: n^k = 36^8 = 2.821.109.907.456
muss es nicht 62^8 sein,da 26 Buchstaben x2 und dann noch die 10 Zahlen ???
Ansonsten: TOP seite