1. Einleitung
Hinweis: Dieser Artikel behandelt die abzählende Kombinatorik und setzt der Einfachheit halber die Begriffe „abzählende Kombinatorik” und „Kombinatorik” gleich.
Die Kombinatorik beschäftigt sich mit dem Ermitteln von Anzahlen. Beispiele dafür könnten sein:
- Auf wie viele verschiedene Weisen kann man einen Lottoschein ausfüllen?
- Wenn ein Passwort 8 Zeichen lang sein soll und nur die Buchstaben des Alphabets (26 Stück) zur Verfügung stehen, wie viele mögliche Passwörter können dann gebildet werden?
- Auf wie viele verschiedene Weisen kann ein Hotel eine Gruppe von 12 Personen auf 4 Zimmer aufteilen, wenn in jedem Zimmer maximal 3 Personen Platz haben?
Es gibt zwei verschiedene Verfahren (Variation und Kombination) zur Ermittlung dieser Anzahlswerte, die jeweils zwei „Unterverfahren” (Ziehen ohne Zurücklegen und Ziehen mit Zurücklegen) haben. Um diese Verfahren zu verstehen kann ein Urnenmodell verwendet werden. Stellen wir uns eine Urne vor, die vier Kugeln mit jeweils unterschiedlicher Farbe enthält:
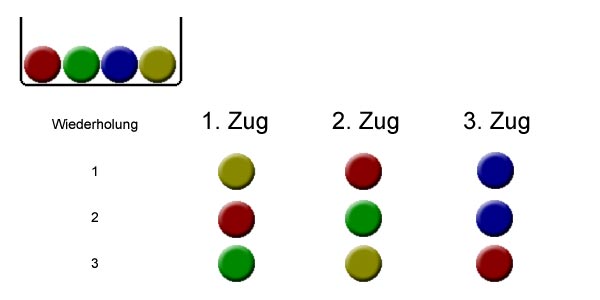
Aus dieser Urne ziehen wir nun drei mal. Einige der möglichen Ergebnisse könnten z. B. sein:
Bei diesen Zügen haben wir ohne Zurücklegen gezogen. Wir haben also eine Kugel aus der Urne genommen, uns die Farbe notiert und die Kugel zur Seite gelegt. Jede Kugel kann dadurch nur maximal ein mal gezogen werden. Beim Ziehen mit Zurücklegen wird die Kugel wieder zurück in die Urne gelegt. Dadurch ist es möglich, die selbe Kugel mehrmals zu ziehen.
Das Ergebnis des Ziehens kann nun auf zwei verschiedene Weisen gezählt werden:
- Mit Beachtung der Reihenfolge (geordnet): Entsprechend des Namens ist es bei dieser Zählweise wichtig in welcher genauen Reihenfolge die Kugeln gezogen wurden. „Erst rot und dann blau” ist also etwas anderes als „erst blau, dann rot”. Man sagt hier auch, dass die verschiedenen möglichen Anordnungen gezählt werden.
- Ohne Beachtung der Reihenfolge (ungeordnet): Genau der umgekehrte Fall — ob zuerst eine rote Kugel gezogen wurde und danach eine blaue oder ob stattdessen erst die blaue und dann die rote Kugel gezogen wurde spielt keine Rolle. Man sagt, dass die verschiedenen Kombinationen gezählt werden. Die Zahl der Kombinationen ist in der Regel geringer als die Zahl der Anordnungen.
Angenommen in einer Urne liegen 6 Kugeln. Auf diesen aufgedruckt sind die Zeichen A, B, C, D, E, F. Zieht man nun mehrmals hintereinander 3 Kugeln (ohne Zurücklegen) aus der Urne, dann könnten sich folgende Anordnungen ergeben:
- (1) A, B, C
- (2) A, F, E
- (3) C, B, F
- (4) B, C, A
- (5) C, B, F
2. Mit/ohne Beachtung der Reihenfolge bzw. geordnet/ungeordnet
Angenommen es wird aus einer Urne gezogen in der fünf Kugeln liegen, welche die Zeichen A, B, C, D und E tragen. Werden nun mehrmals hintereinander jeweils drei Kugeln gezogen, dann können sich verschiedene Anordnungen ergeben. Nachfolgend wird dargestellt, welche dieser Anordnungen gezählt werden würden (grün) und welche nicht (rot).
Mit Beachtung der Reihenfolge / geordnet:
| Ziehung | Beispielhafte Anordnungen | wird gezählt (grün) / wird nicht gezählt (rot) |
|---|---|---|
| 1 | A, B, C | neue Anordnung |
| 2 | B, E, C | neue Anordnung |
| 3 | C, D, A | neue Anordnung |
| 4 | B, C, E | neue Anordnung |
| 5 | A, B, C | bereits durch (1) gezählt |
| 6 | C, A, B | neue Anordnung |
| 7 | D, E, A | neue Anordnung |
| 8 | B, E, C | bereits durch (2) gezählt |
Ohne Beachtung der Reihenfolge / ungeordnet:
| Ziehung | Beispielhafte Anordnungen | wird gezählt (grün) / wird nicht gezählt (rot) |
|---|---|---|
| 1 | A, B, C | neue Anordnung |
| 2 | B, E, C | neue Anordnung |
| 3 | C, D, A | neue Anordnung |
| 4 | B, C, E | bereits durch (2) gezählt |
| 5 | A, B, C | bereits durch (1) gezählt |
| 6 | C, A, B | bereits durch (1) gezählt |
| 7 | D, E, A | neue Anordnung |
| 8 | B, E, C | bereits durch (2) gezählt |
3. Ziehen ohne Zurücklegen, Ziehen mit Zurücklegen
Beim Ziehen ohne Zurücklegen steht jedes Element, das gezogen wurde, für weitere Züge nicht mehr zur Verfügung. Beim Ziehen mit Zurücklegen ist es genau umgekehrt: das Element kann nach dem Ziehen noch mal gezogen werden (und danach wieder noch mal und noch mal usw.).
Die beiden nachfolgenden Tabellen spielen das beispielhaft durch. Wir denken uns wieder eine Urne mit vier Kugeln auf denen die Buchstaben A, B, C und D aufgedruckt sind. Wir ziehen in diesem Beispiel vier mal.
Ziehen ohne Zurücklegen:
| Inhalt der Urne vor dem Zug | Beispielhaft gezogene Kugel | Inhalt der Urne nach dem Zug | Gezogene Anordnung |
| A, B, C, D | C | A, B, C, D | C (+C) |
| A, B, C, D | D | A, B, C, D | C, D (+D) |
| A, B, C, D | A | A, B, C, D | C, D, A (+A) |
| A, B, C, D | B | A, B, C, D | C, D, A, B (+B) |
Ziehen mit Zurücklegen:
| Inhalt der Urne vor dem Zug | Beispielhaft gezogene Kugel | Inhalt der Urne nach dem Zug | Gezogene Anordnung |
| A, B, C, D | C | A, B, C, D | C (+C) |
| A, B, C, D | D | A, B, C, D | C, D (+D) |
| A, B, C, D | C | A, B, C, D | C, D, C (+C) |
| A, B, C, D | C | A, B, C, D | C, D, C, C (+C) |
4. Die verschiedenen Verfahren
Zum Berechnen der unterschiedlichen Anordnungen bzw. Reihenfolgen wird die sogenannte Variation verwendet. Zum Berechnen der Anzahl der unterschiedlichen Kombinationen hingegen wird die Kombination verwendet.
Das ganze noch mal als Tabelle (jeweils mit drei verschiedenen Formulierungen wozu das Verfahren da ist — die Formulierungen bedeuten aber letztlich alle das selbe (pro Spalte)):
| Variation | Kombination |
|---|---|
| Zählt die verschiedenen Anordnungen bzw. beachtet die Reihenfolge bzw. geordnet |
Zählt die verschiedenen Kombinationen bzw. ignoriert die Reihenfolge bzw. ungeordnet |
Hinweis: Bei den meisten Erklärungen zur Kombinatorik wird auch noch die Permutation getrennt genannt. Darauf wird hier verzichtet, da die Permutation nichts anderes als eine spezielle Form der Variation ist. (Siehe dazu den Artikel zur Variation und Permutation.)
5. Übersicht: Wann werden Variation, Permutation oder Kombination verwendet?
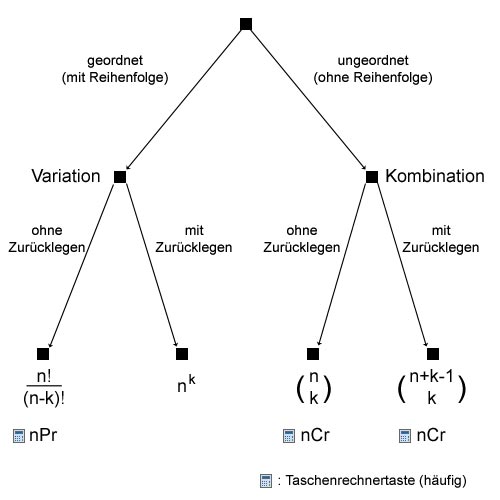
Bereits zuvor wurde beschrieben, wann genau eine Variation und wann eine Kombination verwendet werden soll. Nun folgt das ganze noch mal übersichtlicher als Grafik:
Übersicht Kombinatorik.
Zeigt, ob Variation oder Kombination verwendet werden soll,
abhängig vom Zurücklegen (mit/ohne Zurücklegen)
und abhängig von der Zählweise der Anordnung (mit/ohne Reihenfolge).
Angegeben ist jeweils auch die Formel.
Unter der Formel steht die Taste, die zumeist bei Taschenrechnern die Berechnung abkürzt
(mehr dazu steht im jeweiligen Artikel).
Zeigt, ob Variation oder Kombination verwendet werden soll,
abhängig vom Zurücklegen (mit/ohne Zurücklegen)
und abhängig von der Zählweise der Anordnung (mit/ohne Reihenfolge).
Angegeben ist jeweils auch die Formel.
Unter der Formel steht die Taste, die zumeist bei Taschenrechnern die Berechnung abkürzt
(mehr dazu steht im jeweiligen Artikel).
Hinweis: Die Permutation ist zur Vereinfachung nicht in der Grafik enthalten, da es sich um eine spezielle Form der Variation handelt (durch Einsetzen der Zahlen erhält man automatisch die Permutationsformel). Das heißt, dass man für eine Permutation einfach den selben Pfad wie bei der Variation folgen muss. Tipp: Bei Permutationen wird immer ohne Zurücklegen gezogen.
6. Fakultät
Sowohl die Variation als auch die Kombination greifen auf die sogenannte Fakultät zurück. Die Fakultät wird durch ein Ausrufezeichen hinter einer Zahl kenntlich gemacht. Liegt etwa die Zahl n vor, dann heißt n! ausgeprochen „Fakultät von n”. Die Berechnung erfolgt nach folgender Regel:
Beispiel 1 (Fakultät von 3): 3! = 3*2*1 = 6
Beispiel 2 (Fakultät von 7): 7! = 7*6*5*4*3*2*1 = 5040
Beispiel 3 (Fakultät von 12): 12! = 12*11*10*9*8*7*6*5*4*3*2*1 = 479.001.609
Wie zu sehen ist, wird die Fakultät schnell sehr groß! Daher sollte man immer einen Taschenrechner griffbereit haben, der die Fakultät einer Zahl ausrechnen kann. Genauso wie bei der Schreibweise wird auch beim Taschenrechner gewöhnlich zuerst die Zahl eingegeben und dann das Fakultätszeichen. Etwa 7, !, = für die Fakultät von 7.
Besondere Fälle:
Fakultät von 1: 1! = 1 (das ist noch intuitiv)
Fakultät von 0: 0! = 1 (!)
Die Fakultät der Zahl 0 ist 1 und NICHT 0. Das sollte man sich merken, denn mit hoher Wahrscheinlichkeit wird man früher oder später einmal auf „0!” treffen.
Es gilt: 0! = 1 (Fakultät von 0 ist gleich 1)
6.1. Tipp: Fakultäten und Brüche
Mitunter trifft man auf Brüche, die sowohl im Zähler als auch im Nenner Fakultäten haben. Wenn man keinen Taschenrechner verwenden darf oder wenn die Zahlen so groß werden, dass der Taschenrechner sie nicht mehr handhaben kann (passiert bei Fakultäten schnell mal), dann kann man sich auch mittels Kürzen helfen. Beispiel:
Kommentare (4)
Von neu nach altWir bitten um ihr Verständnis.
Beispiel korrigiert
Das Beisüpiel scheint mir schlecht gewählt zu sein, da man bekanntlicher weise aus Summen nicht kürzen darf.
Ohne Kürzen ergibt der Bruch ungefähr 105; mit Kürzen soll 107 herauskommen?!