Schnellübersicht
Zuvor wurden die Begriffe Zufallsexperiment, Elementarereignis und Ereignis beschrieben. Nun soll ein einfacher Weg erklärt werden, wie man die Wahrscheinlichkeit eines Ereignisses bestimmt (funktioniert aber nicht für alle Zufallsexperimente).
Zunächst sollte man dazu wissen, dass die Wahrscheinlichkeit mathematisch mit „P” abgekürzt wird (probability) und immer zwischen 0 und 1 liegt (0 = 0% Wahrscheinlichkeit / tritt nie ein, 1 = 100% Wahrscheinlichkeit / tritt immer ein).
Beispiel: Stellen wir uns einen Münzwurf als Zufallsexperiment vor. Wir wollen nun die Wahrscheinlichkeiten dafür beschreiben, dass ein Wappen (Ereignis 1) oder eine Zahl (Ereignis 2) geworfen wird. Daher definieren wir die Ereignisse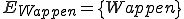 und
und 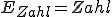 (und setzen als bekannt voraus, dass jede Seite in 50% aller Fälle geworfen wird).
(und setzen als bekannt voraus, dass jede Seite in 50% aller Fälle geworfen wird).
Es gilt nun:
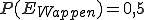 und
und 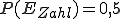 .
.
Wie kommt man aber nun auf 0,5 bzw. 50% für jede der Münzseiten? Genau dafür wird die sogenannte Laplace-Wahrscheinlichkeit verwendet (wird auch als klassische Definition der Wahrscheinlichkeit oder als Laplace-Formel bezeichnet). Sie stammt von Pierre Simon Laplace, einem der Pioniere der Wahrscheinlichkeitstheorie. Für ein Ereignis E lautete die Definition:
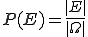
Wir erinnern uns: Ω ist der Ergebnisraum, also die Menge aller möglichen Elementarereignisse. |X| wiederum gibt die Anzahl aller Elemente in der Menge X wieder (z. B. ergibt |Ω| die Anzahl aller möglichen Elementarereignisse und |E| die Anzahl aller Elementarereignisse im Ereignis E).
Vereinfacht ausgedrückt lautet die Formel daher:
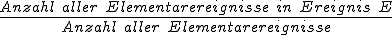
Beispiel 1: Beim Münzwurf gibt es zwei Elementarereignisse: Wappen und Zahl. Der Ergebnisraum Ω lautet daher {Wappen, Zahl} und |Ω| ist 2. Berechnen wir nun die Wahrscheinlichkeiten für die zuvor erwähnten Ereignisse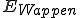 und
und 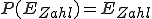 (welche jeweils nur ein Elementarereignis, nämlich Wappen oder Zahl enthalten), dann gilt:
(welche jeweils nur ein Elementarereignis, nämlich Wappen oder Zahl enthalten), dann gilt:
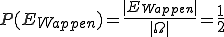 und
und 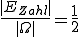
Beispiel 2: Beim Würfelwurf gibt es insgesamt 6 Elementarereignisse. Daher gilt für Ω = {1, 2, 3, 4, 5, 6} und |Ω| = 6. Definieren wir nun das Ereignis E, dass eine 6 gewürfelt wird (E = {6}), dann gilt:
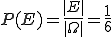 .
.
Beispiel 3: Das Ereignis für das die Wahrscheinlichkeit bestimmt werden soll darf auch mehr als ein Elementarereignis enthalten. So können wir für den Würfelwurf definieren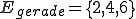 (das Ereignis, dass eine gerade Augenzahl gewürfelt wird). Die Wahrscheinlichkeit für dieses Ereignis errechnet sich dann wie folgt:
(das Ereignis, dass eine gerade Augenzahl gewürfelt wird). Die Wahrscheinlichkeit für dieses Ereignis errechnet sich dann wie folgt:
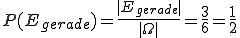 .
.
Beim Münz- und Würfelwurf funktioniert die Anwendung der Laplace-Formel prima. Bei vielen anderen Zufallsexperimenten allerdings nicht. Sie kann nur dann angewendet werden, wenn alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben. Bei der Münze und beim Würfel ist das gegeben: Per Zufall erscheint eine der Seiten und keine hat eine höhere Wahrscheinlichkeit als irgendeine andere Seite. Bereits bei einem gezinkten Würfel, der z. B. in 50% aller Fälle eine 6 ergibt und in 50% aller Fälle eine Augenzahl zwischen 1 und 5 versagt die Laplace-Formel.
Wieso kann die Formel nun nicht auf solche Zufallsexperimente angewendet werden? Das liegt daran, dass in der Formel nur die Anzahlen eine Rolle spielen: Die Anzahl aller gesuchten Elementarereignisse wird durch die Anzahl aller möglichen Elementarereignisse geteilt. Verwendet man nur die Anzahlswerte, dann setzt man voraus, dass die Eintrittswahrscheinlichkeit jedes einzelnen Elementarereignisses gleich ist — andernfalls müssten auch die Eintrittswahrscheinlichkeiten der Elementarereignisse in der Formel auftauchen.

Wir haben zuvor immer nur die Wahrscheinlichkeit berechnet, dass ein bestimmtes Ereignis eintritt. Genauso kann auch berechnet werden wie hoch die Wahrscheinlichkeit ist, dass das Gegenteil passiert: das sogenannte Gegenereignis. Es wird mit einem horizontalen Strich gekennzeichnet, z. B. ist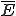 das Gegenereignis zu E.
das Gegenereignis zu E.
Die Wahrscheinlichkeit, dass das Gegenereignis eintritt ist immer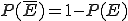 . Z. B. gilt für den Münzwurf
. Z. B. gilt für den Münzwurf  (was genau der Wahrscheinlichkeit entspricht, dass eine Zahl geworfen wird). Das Gegenereignis ist manchmal einfacher zu berechnen als das eigentlich gesuchte Ereignis — das sollte man sich bei Aufgaben zunutze machen und über den Umweg des Gegenereignisses das eigentliche Ergebnis errechnen.
(was genau der Wahrscheinlichkeit entspricht, dass eine Zahl geworfen wird). Das Gegenereignis ist manchmal einfacher zu berechnen als das eigentlich gesuchte Ereignis — das sollte man sich bei Aufgaben zunutze machen und über den Umweg des Gegenereignisses das eigentliche Ergebnis errechnen.
Beispiel: Wie hoch ist die Wahrscheinlichkeit, dass bei einem Würfelwurf eine Augenzahl größer als 1 gewürfelt wird?
Wir definieren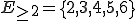 . Daher gilt auch
. Daher gilt auch 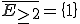 .
.
Wir rechnen:
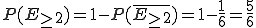
Bei diesem vergleichsweise einfachen Beispiel wäre es vermutlich genauso schnell gegangen, die Wahrscheinlichkeit auf normalem Weg auszurechnen. Später gibt es aber Aufgabenstellungen, bei denen die Berechnungen schnell sehr kompliziert werden, sodass jedes Elementarereignis, das beim Rechnen nicht beachtet werden muss, einem viel Zeit einspart.
Es gibt noch einige Regeln für die Wahrscheinlichkeitsrechnung, die sich letztlich aus dem ableiten, was zuvor beschrieben wurde. (Stehen hier eher der Vollständigkeit halber.)





- P(E) ist die mathematische Schreibweise für „Wahrscheinlichkeit des Ereignisses E”. Wahrscheinlichkeiten liegen zwischen 0 und 1 (entspricht 0% bis 100%).
- Laplace-Formel: Liegt ein Ereignis E und der Ergebnisraum Ω vor, dann gilt
, sofern alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben (ist z. B. beim Würfelwurf der Fall).
- Das Ereignis, das immer dann eintritt, wenn E nicht eintritt ist
(Gegenereignis zu E). Es gilt
. Manchmal ist P(
) leichter zu berechnen als P(E).
1. Einleitung
Zuvor wurden die Begriffe Zufallsexperiment, Elementarereignis und Ereignis beschrieben. Nun soll ein einfacher Weg erklärt werden, wie man die Wahrscheinlichkeit eines Ereignisses bestimmt (funktioniert aber nicht für alle Zufallsexperimente).
Zunächst sollte man dazu wissen, dass die Wahrscheinlichkeit mathematisch mit „P” abgekürzt wird (probability) und immer zwischen 0 und 1 liegt (0 = 0% Wahrscheinlichkeit / tritt nie ein, 1 = 100% Wahrscheinlichkeit / tritt immer ein).
Beispiel: Stellen wir uns einen Münzwurf als Zufallsexperiment vor. Wir wollen nun die Wahrscheinlichkeiten dafür beschreiben, dass ein Wappen (Ereignis 1) oder eine Zahl (Ereignis 2) geworfen wird. Daher definieren wir die Ereignisse
Es gilt nun:
2. Laplace-Wahrscheinlichkeit
Wie kommt man aber nun auf 0,5 bzw. 50% für jede der Münzseiten? Genau dafür wird die sogenannte Laplace-Wahrscheinlichkeit verwendet (wird auch als klassische Definition der Wahrscheinlichkeit oder als Laplace-Formel bezeichnet). Sie stammt von Pierre Simon Laplace, einem der Pioniere der Wahrscheinlichkeitstheorie. Für ein Ereignis E lautete die Definition:
Wir erinnern uns: Ω ist der Ergebnisraum, also die Menge aller möglichen Elementarereignisse. |X| wiederum gibt die Anzahl aller Elemente in der Menge X wieder (z. B. ergibt |Ω| die Anzahl aller möglichen Elementarereignisse und |E| die Anzahl aller Elementarereignisse im Ereignis E).
Vereinfacht ausgedrückt lautet die Formel daher:
Beispiel 1: Beim Münzwurf gibt es zwei Elementarereignisse: Wappen und Zahl. Der Ergebnisraum Ω lautet daher {Wappen, Zahl} und |Ω| ist 2. Berechnen wir nun die Wahrscheinlichkeiten für die zuvor erwähnten Ereignisse
Beispiel 2: Beim Würfelwurf gibt es insgesamt 6 Elementarereignisse. Daher gilt für Ω = {1, 2, 3, 4, 5, 6} und |Ω| = 6. Definieren wir nun das Ereignis E, dass eine 6 gewürfelt wird (E = {6}), dann gilt:
Beispiel 3: Das Ereignis für das die Wahrscheinlichkeit bestimmt werden soll darf auch mehr als ein Elementarereignis enthalten. So können wir für den Würfelwurf definieren
2.1. Wann die Laplace-Formel nicht gilt
Beim Münz- und Würfelwurf funktioniert die Anwendung der Laplace-Formel prima. Bei vielen anderen Zufallsexperimenten allerdings nicht. Sie kann nur dann angewendet werden, wenn alle Elementarereignisse die selbe Eintrittswahrscheinlichkeit haben. Bei der Münze und beim Würfel ist das gegeben: Per Zufall erscheint eine der Seiten und keine hat eine höhere Wahrscheinlichkeit als irgendeine andere Seite. Bereits bei einem gezinkten Würfel, der z. B. in 50% aller Fälle eine 6 ergibt und in 50% aller Fälle eine Augenzahl zwischen 1 und 5 versagt die Laplace-Formel.
Wieso kann die Formel nun nicht auf solche Zufallsexperimente angewendet werden? Das liegt daran, dass in der Formel nur die Anzahlen eine Rolle spielen: Die Anzahl aller gesuchten Elementarereignisse wird durch die Anzahl aller möglichen Elementarereignisse geteilt. Verwendet man nur die Anzahlswerte, dann setzt man voraus, dass die Eintrittswahrscheinlichkeit jedes einzelnen Elementarereignisses gleich ist — andernfalls müssten auch die Eintrittswahrscheinlichkeiten der Elementarereignisse in der Formel auftauchen.
Die Laplace-Formel darf nur dann verwendet werden, wenn jedes Elementarereignis die selbe Eintrittswahrscheinlichkeit hat (siehe z. B. Würfel oder Münzwurf).
3. Gegenereignis
Wir haben zuvor immer nur die Wahrscheinlichkeit berechnet, dass ein bestimmtes Ereignis eintritt. Genauso kann auch berechnet werden wie hoch die Wahrscheinlichkeit ist, dass das Gegenteil passiert: das sogenannte Gegenereignis. Es wird mit einem horizontalen Strich gekennzeichnet, z. B. ist
Die Wahrscheinlichkeit, dass das Gegenereignis eintritt ist immer
Beispiel: Wie hoch ist die Wahrscheinlichkeit, dass bei einem Würfelwurf eine Augenzahl größer als 1 gewürfelt wird?
Wir definieren
Wir rechnen:
Bei diesem vergleichsweise einfachen Beispiel wäre es vermutlich genauso schnell gegangen, die Wahrscheinlichkeit auf normalem Weg auszurechnen. Später gibt es aber Aufgabenstellungen, bei denen die Berechnungen schnell sehr kompliziert werden, sodass jedes Elementarereignis, das beim Rechnen nicht beachtet werden muss, einem viel Zeit einspart.
4. Grundsätzliche Regeln
Es gibt noch einige Regeln für die Wahrscheinlichkeitsrechnung, die sich letztlich aus dem ableiten, was zuvor beschrieben wurde. (Stehen hier eher der Vollständigkeit halber.)
: Die Wahrscheinlichkeit eines Ereignisses P(E) liegt immer zwischen 0 und 1 (entspricht 0% bis 100% Wahrscheinlichkeit).
: Die Wahrscheinlichkeit des sicheren Ereignisses beträgt 1. Das sichere Ereignis tritt also immer ein. (Anders formuliert: Die Wahrscheinlichkeit, irgendeines der möglichen Elementarereignisse zu erhalten beträgt 1.)
: Die Wahrscheinlichkeit des unmöglichen Ereignisses beträgt 0 (man erhält immer mindestens ein Elementarereignis). Statt P({}) kann auch P(∅) geschrieben werden.
5. Quiz
Welcher Buchstabe repräsentiert gewöhnlich die Wahrscheinlichkeit?
X (z. B. X(E))
W (z. B. W(E))
A (z. B. A(E))
P (z. B. P(E))
Zwischen welchen exakten Werten darf eine berechnete Wahrscheinlichkeit gewöhnlich liegen?
-100 bis 100
0 bis 100
1 bis 100
0 bis 1
Angenommen man hat ein Ereignis E das aus mehreren Elementarereignissen besteht und den Ereignisraum Ω. Wie berechnet sich die Wahrscheinlichkeit des Ereignisses E unter Verwendung der Laplace-Formel?
|E|+|Ω|+1
|1 - (|E| geteilt durch |Ω|)
|Ω| geteilt durch |E
|E| geteilt durch |Ω|
Angenommen man hat zu einem Würfelwurf die Ereignisse E1 = {1, 2} und E2 = {3, 4, 5, 6}. Wie kann E2 dann auch bezeichnet werden?
Polarisationsereignis zu E1
Normalenreignis zu E1
Spiegelereignis zu E1
Gegenreignis zu E1
Wie berechnet sich die Wahrscheinlichkeit des Gegenereignisses zum Ereignis E?
(P(E))2 - 1
-1 + P(E)
1 + P(E)
1 - P(E)
6. Links
- Laplace-Formel: Wikipedia, Brinkmann, OberPrima (Video)
- Gegenereignis
Kommentare (6)
Von neu nach altWir bitten um ihr Verständnis.
Ich denke nicht!!! ^
/ 0 \
------
folgende 2 beispiele:
a.) 11 kugeln. eine rot, rest schwarz. es wird EINMAL gezogen. wahrscheinlichkeit somit 1:10
b.) 12 kugeln. eine rot, rest schwarz. es wird DREIMAL gezogen (kugel wird jedesmal zurückgelegt). wahrscheinlichkeit somit 1:11, das aber drei mal.
ist es nun möglich zu berechnen, bei welcher der beiden varianten es am ende wahrscheinlicher ist die rote zu ziehen oder ist die warscheinlichkeit bei variante b tatsächlich immer geringer, EGAL wie oft man zieht?
1:10 zu 1:??
müsste dann eigentlich so aussehen: 1:10 zu 3x1:11 >> kürzen/berechnen/vergleichen?
bei einer einmaligen ziehung von variante b ist die sache klar. aber bei mehreren malen?
danke.
Ansonsten ist alles Super ;))