Schnellübersicht
Bisher wurden Zufallsexperimente stets als ein einzelner Vorgang dargestellt, der beliebig oft wiederholt werden kann (z. B. ein Münzwurf, der mehrmals hintereinander ausgeführt wird). Es ist aber auch möglich, mehrere Vorgänge in einem Zufallsexperiment nacheinander durchzuführen. Man spricht dann von einem mehrstufigen Zufallsexperiment. Ein derartiges mehrstufiges Zufallsexperiment lässt sich in einem Baumdiagramm darstellen. Dieses besteht aus einem „Startpunkt” von welchem „Zweige” zu weiteren Punkten abgehen. Jeder Punkt repräsentiert ein mögliches Elementarereignis eines Vorgangs. An die „Zweige” werden die Wahrscheinlichkeiten des jeweiligen Elementarereignisses geschrieben.
Die Wahrscheinlichkeiten werden an die Kanten geschrieben (hier 1/2 beim Münzwurf und 1/6 beim Würfelwurf). Am Ende stehen die Elementarereignisse des gesamten mehrstufigen Zufallsexperiments.
Wir können nun folgendes Baumdiagramm bilden:
Wie darin zu erkennen ist, kann beim ersten Zug entweder eine rote oder eine blaue Kugel gezogen werden. Es gibt zwei rote Kugeln und insgesamt drei, daher ist P(Erot) = 2/3. Wurde nun im ersten Zug eine blaue Kugel gezogen, dann gibt es nur noch (zwei) rote Kugeln und die Wahrscheinlichkeit eine rote zu ziehen steigt auf 1. Wurde hingegen im ersten Zug eine rote Kugel gezogen, dann gibt es anschließend exakt eine rote und eine blaue Kugel in der Urne. Beide haben entsprechend eine Wahrscheinlichkeit gezogen zu werden von 0,5.
Das Baumdiagramm hilft nun nicht nur einfach bei der Darstellung des Problems, sondern auch bei der Berechnung. Es gelten folgende zwei Regeln:
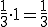 und für {rot, blau} der Wert
und für {rot, blau} der Wert 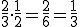 .
.
Definiert man nun das Ereignis Er={{blau, rot}, {rot, blau}} (exakt eine rote Kugel), dann ergibt sich die Wahrscheinlichkeit aus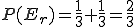 .
.
- Mehrstufiges Zufallsexperiment: Es werden mehrere (i. d. R. unterschiedliche) Vorgänge nacheinander ausgeführt (statt nur einer, welcher immer wieder wiederholt wird).
- Mehrstufige Zufallsexperimente können mittels Baumdiagramm abgebildet werden (Knoten=Elementarereignisse, Kanten führen zu gültigem nächsten Elementarereignis).
- 1. Pfadregel: Die Wahrscheinlichkeit eines gesamten Pfades ergibt sich, indem die Wahrscheinlichkeiten aller Abschnitte des Pfades miteinander multipliziert werden.
- 2. Pfadregel: P(E) = P(e1)+P(e2), wenn das Ereignis E die Elementarereignisse e1 und e2 enthält. (Hier sind die Elementarereignisse des gesamten mehrstufigen Zufallsexperiments gemeint, nicht eines einzelnen Vorgangs.)
1. Einleitung
Bisher wurden Zufallsexperimente stets als ein einzelner Vorgang dargestellt, der beliebig oft wiederholt werden kann (z. B. ein Münzwurf, der mehrmals hintereinander ausgeführt wird). Es ist aber auch möglich, mehrere Vorgänge in einem Zufallsexperiment nacheinander durchzuführen. Man spricht dann von einem mehrstufigen Zufallsexperiment. Ein derartiges mehrstufiges Zufallsexperiment lässt sich in einem Baumdiagramm darstellen. Dieses besteht aus einem „Startpunkt” von welchem „Zweige” zu weiteren Punkten abgehen. Jeder Punkt repräsentiert ein mögliches Elementarereignis eines Vorgangs. An die „Zweige” werden die Wahrscheinlichkeiten des jeweiligen Elementarereignisses geschrieben.
2. Beispiel 1
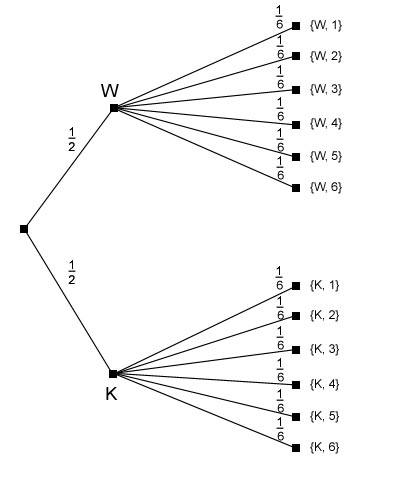
Man wirft erst eine Münze und anschließend einen Würfel. Die Elementarereignisse könnten dann z. B. lauten {Wappen, 1}, {Wappen, 2}, ..., {Zahl, 1}, ..., {Zahl, 6}. Das Baumdiagramm für dieses mehrstufige Zufallsexperiment könnte nun wie folgt aussehen:Die Wahrscheinlichkeiten werden an die Kanten geschrieben (hier 1/2 beim Münzwurf und 1/6 beim Würfelwurf). Am Ende stehen die Elementarereignisse des gesamten mehrstufigen Zufallsexperiments.
3. Beispiel 2
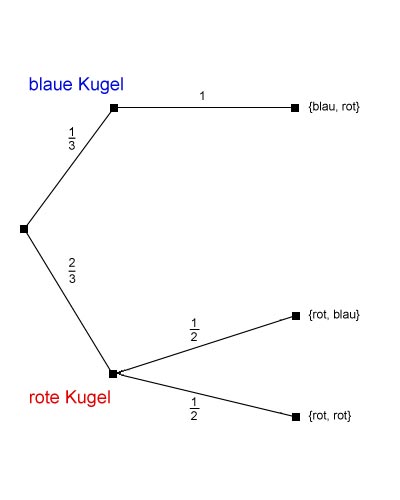
Bei der Verknüpfung von Münz- und Würfelwurf ist das Baumdiagramm noch nicht allzu nützlich, da sich die Wahrscheinlichkeiten nicht mit jedem Schritt verändern. Nachfolgend soll daher ein Beispiel gebildet werden, bei dem die Wahrscheinlichkeiten des zweiten Vorgangs vom Ergebnis des ersten Vorgangs abhängen. Wir stellen uns dazu eine Urne vor, in welcher sich insgesamt drei Kugeln befinden. Zwei davon sind rot, eine ist blau. Wir werden verdeckt aus dieser Urne nacheinander zwei Kugeln ziehen, sodass das Ergebnis jedes einzelnen Zugs vom Zufalls abhängt.Wir können nun folgendes Baumdiagramm bilden:
Wie darin zu erkennen ist, kann beim ersten Zug entweder eine rote oder eine blaue Kugel gezogen werden. Es gibt zwei rote Kugeln und insgesamt drei, daher ist P(Erot) = 2/3. Wurde nun im ersten Zug eine blaue Kugel gezogen, dann gibt es nur noch (zwei) rote Kugeln und die Wahrscheinlichkeit eine rote zu ziehen steigt auf 1. Wurde hingegen im ersten Zug eine rote Kugel gezogen, dann gibt es anschließend exakt eine rote und eine blaue Kugel in der Urne. Beide haben entsprechend eine Wahrscheinlichkeit gezogen zu werden von 0,5.
4. Pfadregeln
Das Baumdiagramm hilft nun nicht nur einfach bei der Darstellung des Problems, sondern auch bei der Berechnung. Es gelten folgende zwei Regeln:
- Die Wahrscheinlichkeit eines Elementarereignisses des mehrstufigen Zufallsexperiments ist gleich dem Produkt der Wahrscheinlichkeiten des Pfades, der zu diesem Elementarereignis führt.
- Die Wahrscheinlichkeit eines Ereignisses ist gleich der Summe aller Elementarereignisse, die Teil des Ereignisses sind.
Definiert man nun das Ereignis Er={{blau, rot}, {rot, blau}} (exakt eine rote Kugel), dann ergibt sich die Wahrscheinlichkeit aus
Kommentare (11)
Von neu nach altWir bitten um ihr Verständnis.