Mit Hilfe des Skalarprodukts ist es möglich, den Winkel zwischen zwei Vektoren zu errechnen. Dazu muss man nur die bereits bekannte Regel
nach Cosinus umstellen:
Es gilt also: Skalarprodukt von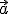
und 
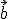durch die miteinander multiplizierten Längen der beiden Vektoren ergibt den Cosinus von 
.
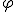Allgemein:
Beispiel:
nach Cosinus umstellen:
Es gilt also: Skalarprodukt von
und durch die miteinander multiplizierten Längen der beiden Vektoren ergibt den Cosinus von .1. Formel
Allgemein:
Beispiel:
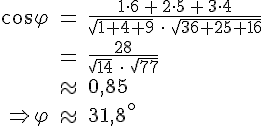
Kommentare (23)
Von neu nach altWir bitten um ihr Verständnis.
Dann ist alpha = cos°-1 * (ankathete/gegenkathete).
Dabei aufpassen, ob man den Winkel in Grad ° (deg) oder Bogenmaß (rad) verwendet.
Beim Tan-1 <-90° oder > 90° aufpassen. Die cos-Formel oben funktioniert nur, falls sich für den Winkel zwischen den Vektoren ein rechtwinkliges Dreieck bilden lässt. Für stumpfe Winkel braucht man eine andere Formel oder muß die Sektoren und vorzeichen manuell zeichnerisch auswerten. Da kommt man ohne rechte Winkel nur über SSS-Dreiecksformel mit dem Rechner ran.
Hier ist erstmal Problemverständnis der Aufgabe wichtig. Also in welche Richtung das erwartete Ergebnis im Verhältnis zu den Eingangsgrößen liegt. Kreisförmige Anordnungen, Rotationsbewegungen oder Schwingungen sind hier sensibel.
Dann ist alpha = cos°-1 * (ankathete/gegenkathete).
Dabei aufpassen, ob man den Winkel in Grad ° (deg) oder Bogenmaß (rad) verwendet.
Beim Tan-1 <-90° oder > 90° aufpassen. Die cos-Formel oben funktioniert nur, falls sich für den Winkel zwischen den Vektoren ein rechtwinkliges Dreieck bilden lässt. Für stumpfe Winkel braucht man eine andere Formel oder muß die Sektoren und vorzeichen manuell zeichnerisch auswerten. Da kommt man ohne rechte Winkel nur über SSS-Dreiecksformel mit dem Rechner ran.
Hier ist erstmal Problemverständnis der Aufgabe wichtig. Also in welche Richtung das erwartete Ergebnis im Verhältnis zu den Eingangsgrößen liegt. Kreisförmige Anordnungen, Rotationsbewegungen oder Schwingungen sind hier sensibel.
Das Ergebnis ist doch das selbe.
Nur auf die Fragestellung achten; daraus kannst du entnehmen welcher winkel gesucht ist