Winkel zwischen Gerade und Gerade (Vektorrechnung)

1. Einleitung

Für den Winkel zwischen zwei Geraden sind ausschließlich deren beiden Richtungsvektoren entscheidend.
Es reicht also, den Winkel zwischen den beiden Richtungsvektoren zu bilden, um den Winkel zwischen den beiden Geraden zu erhalten.

2. Formel

Allgemein:

g_1: vektor x=(s_11, s_12, ..., s_1n) + lambda*(r_11, r_12, ..., r_1n), r_1=(r_11, r_12, ..., r_1n)

g_2: vektor x=(s_21, s_22, ..., s_2n) + lambda*(r_21, r_22, ..., r_2n), r_2=(r_21, r_22, ..., r_2n)

In der letzten Formel (Bruch) errechnet man den Zähler mit Hilfe des
Skalarprodukts und den Nenner mit der

Länge der beiden Vektoren. Das Ergebnis ist der Cosinuswert des Winkels, den man dann mit einem Taschenrechner zur Gradzahl des Winkels umrechnen kann. Ist der Winkel, der sich dadurch ergibt, größer als 90°, dann muss man 180° minus errechneter Winkel rechnen (siehe Anmerkungen).

Beispiel:

cos(phi)=(|(5,6,7)*(2,2,2)|)/(|(5,6,7)|*|(2,2,2)|)=36/1320= ca. 0,991 entspricht phi = ca. 7,75 Grad

3. Anmerkungen

Bevor man den Winkel zwischen zwei Geraden ausrechnet sollte man überprüfen, ob sich die Geraden überhaupt schneiden.

Schneiden sich zwei Vektoren, dann kann man immer einen spitzen und einen stumpfen Winkel errechnen (also einen kleineren und einen größeren Winkel).
Beide Winkel addiert ergeben immer 180°.
Gesucht wird in der Regel der spitze Winkel.
Sollte man also einen Winkel erhalten, der größer als 90° ist, dann muss man 180° minus errechneter Winkel rechnen, um so den spitzen Winkel zu erhalten.

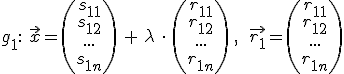
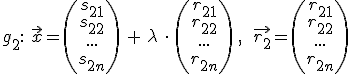
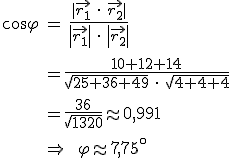
Kommentare (8)

Von neu nach alt

Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.

penis

eine Methode den Schnittwinkel von 2 Geraden im 2-dimensionalen Raum wäre mithilfe des steigungsdreiecks die einzelnen Winkel ausrechenen oder tan(alpha)=Steigung und das nach alpha auflösen. Jetzt nimmt man einen der Winkel und rechnet 180°-Winkel udn erhält ein Ergebnis. Dann Ergebnis - 2. Winkel = Schnittwinkel

Bei der Methode bin ich mir aber nicht sicher von daher bin ich froh wenn mich jemand korrigiert falls es falsch ist.

wobei ich die variablen vor den Vektoren anders benennen würde, um Missverständnisse außzuschließen.

doch sie schneiden sich für lambda(g1)= -1 und lambda(g2) = -2,5

Leider Schneiden sich die Geraden garnicht..

das mit dem winkel ist klar...

wir hatten richtungsvektoren noch nicht im

unterricht, weiß auch nicht, was das genau ist..

kann man trotzdem den winkel zwischen 2 geraden

ausrechnen? müsste eig auch anders gehen,

da wir das - wie gesagt - noch nicht hatten..

schreib gleich mathe, bitte um schnelle antwort^^

Der Betrag garantiert nur, dass der berechnete Winkel nicht stumpf ist

also soweit ist das klar, aber wieso steht hier bei der formel im zähler (also beim skalarprodukt) die beiden vektoren im betragsstrichen. bei den anderen berrechnungen also ebene ebene und so ist das nämlich nicht so..

Winkel zwischen Gerade und Gerade (Thema: Vektorrechnung)

Wie man den Winkel zwischen einer Geraden und einer Geraden errechnet

1. Einleitung

2. Formel

3. Anmerkungen

Kommentare (8)