Einleitung (Thema: Vektorrechnung)

Bei der Berechnung von Winkeln in der Vektorrechnung taucht immer wieder die Formel des Skalarprodukts auf:




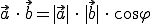
Wie leicht zu erkennen ist, ist nämlich in dieser Formel der Winkel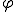 enthalten - und zwei Vektoren. Stellt man die Formel also um, so kann man schnell den Winkel 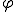zwischen diesen beiden Vektoren errechnen!

Umgestellt:

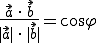
Den Cosinuswert des Winkels kann man dann einfach im Taschenrechner zur Gradzahl umrechnen. Die genannte Formel wird immer wieder bei der Winkelberechnung verwendet und sollte daher gut beherrscht werden.



Als Vektor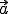 und 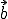verwendet man

• Bei Winkeln zwischen Vektoren einfach die Vektoren selbst.
• Bei Winkeln zwischen Geraden deren Richtungsvektoren.
• Bei Winkeln zwischen Ebenen deren Normalenvektoren.

Das ganze kann natürlich dann auch vermischt werden: Bei einem Winkel zwischen Ebene und Gerade z.B. ein Normalenvektor (Ebene) und ein Richtungsvektor (Gerade).



Weiterhin gilt es bei der Winkelberechnung noch zwei wichtige Faktoren zu beachten:

• Der errechnete Winkel ist nicht immer gleich der gesuchte Winkel! Der Winkel zwischen den Normalenvektoren von zwei Ebenen ist z.B. nicht gleich dem Winkel zwischen den Ebenen. Aber wenn dies der Fall ist, dann lässt es sich immer leicht umrechnen (bei Ebenen z.B. 90° minus errechneter Winkel). Hat man vergessen, was man wovon abziehen muss, dann kann eine Skizze helfen in der man sich verdeutlicht, welchen Winkel man da eigentlich gerade ausgerechnet hat.
• Bevor man einen Winkel errechnet sollte man schauen, ob überhaupt ein Winkel existiert. Bei windschiefen Geraden kann man z.B. auch einen Winkel errechnen, obwohl sich diese nie schneiden.