auch genannt: Kreuzprodukt
Das Thema Vektorprodukt wird in der Schule zumeist erst gegen Ende der Unterrichtsreihe "Vektorrechnung" durchgenommen.
Nichtsdestotrotz kann man es aber immer wieder verwenden, sobald regelmäßiger mit Ebenen gerechnet wird.
Mit Hilfe des Vektorprodukts lässt sich nämlich zu jeder Ebene schnell ein Normalenvektor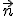 finden, solange zwei Vektoren bekannt sind, die in der Ebene liegen (z.B. die beiden Richtungsvektoren in der Parameterform).
finden, solange zwei Vektoren bekannt sind, die in der Ebene liegen (z.B. die beiden Richtungsvektoren in der Parameterform).
Das Vektorprodukt selbst ist also immer ein Vektor - anders als bei der Skalarmultiplikation, wo das Ergebnis immer ein Skalar ist.
Um das Vektorprodukt zu erhalten, benötigt man zwei Vektoren.
Man rechnet in diesem Fall
Sprich: Vektor a kreuz Vektor b.
Will man das Ergebnis des Vektorprodukts erhalten, so kann man rechnen
In diesem Fall wäre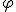 der Winkel, der von
der Winkel, der von 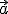 und
und 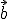 eingeschlossen wird und
eingeschlossen wird und 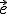 der Einheitsvektor, der zu beiden Vektoren senkrecht liegt.
der Einheitsvektor, der zu beiden Vektoren senkrecht liegt.
Klingt schwierig - isses auch. Aber zum Glück gibt es eine deutlich einfachere Formel, um das ganze auszurechnen, die auch nachfolgend vorgestellt wird.
Allgemein:
Hat man alle Rechnungen durchgeführt, so erhält man einen neuen Vektor.
Die Formel sieht auf den ersten Blick recht kompliziert aus, ist aber sehr leicht auszurechnen (nur Multiplikation und Subtraktion).
Das Merken der Formel ist dafür etwas schwieriger. Wie leicht zu erkennen ist, multipliziert man immer jeweils zwei Komponenten miteinander und zieht die Ergebnisse dann voneinander ab -
so erhält man stückchenweise in drei Rechenschritten die drei Komponenten des neuen Vektors.
Schaut man etwas genauer hin, dann kann man eine Reihe von Regelmäßigkeiten erkennen:
Daraus ergibt sich, dass man sich immer nur zwei der Indizes von jedem Rechenschritt merken muss.
Dann kann man die Formel der Gleichung ohne Indizes aufschreiben und kann diese danach eintragen:
Da die Indizes ja auf der rechten Seite vom Minus aus die gleichen sind, wie auf der linken Seite (nur umgedreht - also statt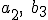 eben
eben 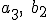 ),
),
reicht es völlig, sich alle Indizes der linken Seite zu merken und einzutragen. Die der rechten Seite ergeben sich dann ja durch umdrehen.
Man trägt also auf der linken Seite jeweils von links oben nach rechts unten ein: 2 33 11 2.
Dadurch ergibt sich folgende Formel:
Fertig! Alles was man sich also für die Formel letztlich merken muss ist: 3 Mal a*b-a*b, Indizes 2 33 11 2 links eintragen, Indizes rechts umdrehen.
Beispiel:
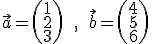
Um das Vektorprodukt auszurechnen, schreiben wir nun zuerst nochmal unsere allgemeine Form der Formel hin (drei mal a*b-a*b, 233112, umdrehen):
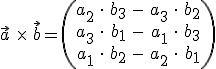
Nun brauchen wir nur noch die Komponenten aus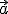 und
und 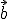 einzusetzen:
einzusetzen:
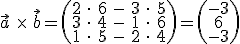
Mit Hilfe des Vektorprodukts kann man sehr schnell Vektoren finden, die orthogonal (also senkrecht) zu zwei anderen Vektoren liegen.
Hat man nun eine Ebene in Parameterform gegeben, so hat man auch immer zwei Richtungsvektoren der Ebene gegeben. Wendet man das Vektorprodukt auf diese an,
so kann man schnell und einfach einen orthogonalen Vektor zu diesen bei Vektoren finden - und damit einen, der auch orthogonal zur Ebene liegt.
Den so gewonnenen Normalenvektor kann man z.B. für Lagebeziehungen oder Abstände verwenden, oder auch um einfach die Normalenform der Ebene zu errechnen.
1. Einleitung
Das Thema Vektorprodukt wird in der Schule zumeist erst gegen Ende der Unterrichtsreihe "Vektorrechnung" durchgenommen.
Nichtsdestotrotz kann man es aber immer wieder verwenden, sobald regelmäßiger mit Ebenen gerechnet wird.
Mit Hilfe des Vektorprodukts lässt sich nämlich zu jeder Ebene schnell ein Normalenvektor
Das Vektorprodukt selbst ist also immer ein Vektor - anders als bei der Skalarmultiplikation, wo das Ergebnis immer ein Skalar ist.
Um das Vektorprodukt zu erhalten, benötigt man zwei Vektoren.
Man rechnet in diesem Fall
Sprich: Vektor a kreuz Vektor b.
Will man das Ergebnis des Vektorprodukts erhalten, so kann man rechnen
In diesem Fall wäre
Klingt schwierig - isses auch. Aber zum Glück gibt es eine deutlich einfachere Formel, um das ganze auszurechnen, die auch nachfolgend vorgestellt wird.
2. Formel
Allgemein:
Hat man alle Rechnungen durchgeführt, so erhält man einen neuen Vektor.
Die Formel sieht auf den ersten Blick recht kompliziert aus, ist aber sehr leicht auszurechnen (nur Multiplikation und Subtraktion).
Das Merken der Formel ist dafür etwas schwieriger. Wie leicht zu erkennen ist, multipliziert man immer jeweils zwei Komponenten miteinander und zieht die Ergebnisse dann voneinander ab -
so erhält man stückchenweise in drei Rechenschritten die drei Komponenten des neuen Vektors.
Schaut man etwas genauer hin, dann kann man eine Reihe von Regelmäßigkeiten erkennen:
- Es wird immer eine Komponente von
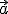 mit einer von
mit einer von 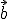 multipliziert - nie zwei Komponenten vom gleichen Vektor.
multipliziert - nie zwei Komponenten vom gleichen Vektor. - Lässt man die Indizes aussen vor, so gilt für jeden Rechenschritt a*b-a*b.
- Betrachtet man die Indizes, dann sieht man, dass in jeden Rechenschritt nur zwei verschiedene Indizes auftauchen. Im ersten 2 und 3, im zweiten 3 und 1 und im dritten 1 und 2.
- Die Indizes drehen sich in jedem Rechenschritt einmal um (z.B. im ersten 2, 3 dann 3, 2).
Daraus ergibt sich, dass man sich immer nur zwei der Indizes von jedem Rechenschritt merken muss.
Dann kann man die Formel der Gleichung ohne Indizes aufschreiben und kann diese danach eintragen:
Da die Indizes ja auf der rechten Seite vom Minus aus die gleichen sind, wie auf der linken Seite (nur umgedreht - also statt
reicht es völlig, sich alle Indizes der linken Seite zu merken und einzutragen. Die der rechten Seite ergeben sich dann ja durch umdrehen.
Man trägt also auf der linken Seite jeweils von links oben nach rechts unten ein: 2 33 11 2.
Dadurch ergibt sich folgende Formel:
Fertig! Alles was man sich also für die Formel letztlich merken muss ist: 3 Mal a*b-a*b, Indizes 2 33 11 2 links eintragen, Indizes rechts umdrehen.
Beispiel:
Um das Vektorprodukt auszurechnen, schreiben wir nun zuerst nochmal unsere allgemeine Form der Formel hin (drei mal a*b-a*b, 233112, umdrehen):
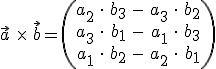
Nun brauchen wir nur noch die Komponenten aus
3. Nutzen des Vektorprodukts
Mit Hilfe des Vektorprodukts kann man sehr schnell Vektoren finden, die orthogonal (also senkrecht) zu zwei anderen Vektoren liegen.
Hat man nun eine Ebene in Parameterform gegeben, so hat man auch immer zwei Richtungsvektoren der Ebene gegeben. Wendet man das Vektorprodukt auf diese an,
so kann man schnell und einfach einen orthogonalen Vektor zu diesen bei Vektoren finden - und damit einen, der auch orthogonal zur Ebene liegt.
Den so gewonnenen Normalenvektor kann man z.B. für Lagebeziehungen oder Abstände verwenden, oder auch um einfach die Normalenform der Ebene zu errechnen.
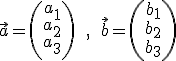
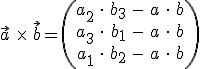
Kommentare (23)
Von neu nach altWir bitten um ihr Verständnis.
Dann ab a 2 jeweils dreimal kreuzweise!! rechnen: ( a 2 * b 3 - a 3 * b 2 / a 3 * b 1 - a 1 * b 3 / a 1 * b 2 - a 2 * b 1 )
Das System läßt sich doch wohl leicht merken
bei der Skalarmultiplikation kommt ein Vektor raus, hier ist wohl das Skalarprodukt gemeint gewesen!
ansonsten gute arbeit!
wenn man beide Vektoren jeweils zweimal untereinander schreibt:
a1 b1
a2 b2
a3 b3
a1 b1
a2 b2
a3 b3
Wenn man jetzt die erste und die letzte Zeile streicht steht da nur noch:
a2 b2
a3 b3
a1 b1
a2 b2
Jetzt ließt man immer über kreuz, erst a2*b3, dann a3*b2, dann a3*b1 usw.
Hört sich jetzt komplizierter an, als es ist... ;) Eigentlich sehr einfach wenn man es mal raus hat.
ist das vektorprodukt jetzt der normalenvektor (wir haben das gar nicht in der schule gemacht)? oder muss man von dem vektorprodukt nochmal den vektor suchen, der orthogonal dazu ist und das ist dann der normalenvektor?
Sprich...
(a2*b3 - a3*b2)
-(!)(a1*b3 - a3*b1)
(a1*b2 - a2*b1)
... ?