Vektoraddition und Vektorsubtraktion (Thema: Vektorrechnung)

Vektoren addieren, subtrahieren, sowie die geometrische Bedeutung

1. Einleitung

Vektoren kann man nahezu genauso einfach wie reelle Zahlen addieren bzw. subtrahieren.
Dazu addiert bzw. subtrahiert man die Koordinatenachsen aller beteiligter Vektoren einzeln und nacheinander.

2. Formel

Allgemein (Addition):

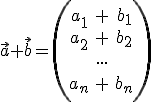
vektor a+vektor b=(a1+b1_a2+b2_..._an+bn)

Allgemein (Subtraktion):

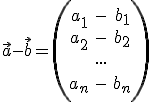
Beispiel (Addition):

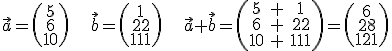
Beispiel (Subtraktion):

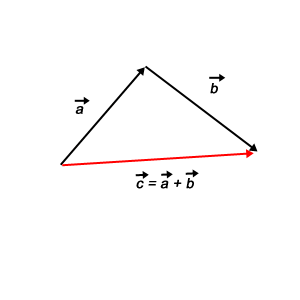
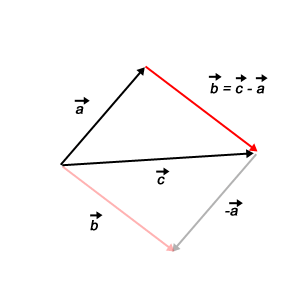
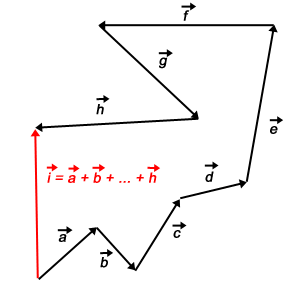
3. Geometrisches Verständnis

Durch die Vektoraddition und -subtraktion kann man gesuchte Vektoren mit Hilfe von anderen Vektoren darstellen. Dies ist insbesondere dann nützlich, wenn man Beweise vektoriell herleiten will oder muss.

Kommentare (4)

Von neu nach alt

Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.

Jep Vektor Sutahiert man anderst, ist hier falsch beschreiben denn man zieht vom rechten den linken ab also b-a

Wow ich kann diese Seite einfach nur loben!!!

Mit der Hilfe, dir einem hier geboten wird, werde sogar ich mein MatheAbi demnächst schaffen :D

Das macht man nur mit Punkten um einen Vektor zu erhalten.

Also mit Punkten wie A(5/3) B (7/4) Der Vektor AB wäre dann (2/1)

Vektoren subtrahiert man so wie es beschrieben ist.

hey, das stimmt doch garnicht..wenn man 2 Vektoren subtrahiert, dann rechnet man Fuß - Spitze!

also vektor a - vektor b = b-a

Um unsere Webseite für Sie optimal zu gestalten und fortlaufend verbessern zu können, verwenden wir Cookies. Durch die weitere Nutzung der Webseite stimmen Sie der Verwendung von Cookies zu. Weitere Informationen zu Cookies erhalten Sie in unserer Datenschutzerklärung. OK