1. Einleitung
Das errechnen eines Vektors aus zwei vorgegebenen Punkten ist eine der häufigsten Aufgaben in der Vektorrechnung - aber glücklicherweise wohl auch die Einfachste.
Um den gesuchten Vektor zu erhalten, braucht man zuerst lediglich die beiden Ortsvektoren zu Punkt A und Punkt B. Dann zieht man den Vektor zu Punkt B vom Vektor zu Punkt A ab - und man erhält den neuen Vektor von A nach B.
Wiederholung: Ortsvektor
Sucht man den Ortsvektor zu einem Punkt P (1|1|1), so kann man dessen Koordinaten einfach identisch für den Ortsvektor weiterverwenden. Man muss sie nur entsprechend der Vektorschreibweise untereinander und in Klammern schreiben:
2. Formel
Allgemein:
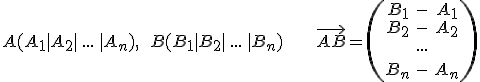
Beispiel:
3. Eselsbrücken
- "Das Vektoralphabet geht von Z-A"
entspricht: Zielpunkt minus Anfangspunkt (=Z-A)
- 2 - 1 = 1
entspricht: Zweiter Punkt minus erster Punkt = 1 Vektor
Kommentare (14)
Von neu nach altWir bitten um ihr Verständnis.
funktioniert immer :)
Vektor: AB = OB-OA
also "Vektor zu A von Vektor zu B abziehen"
Eine Andere Eselsbrücke wäre übrigends das gute alte:
"Rechts vor links" (entspricht: rechten Vektor nehmen, linken Vektor abziehen)