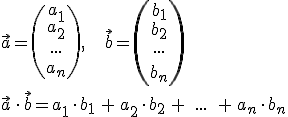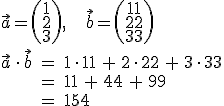Skalarprodukt (Thema: Vektorrechnung)

auch genannt: inneres Produkt

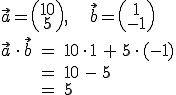
1. Einleitung

Beim Skalarprodukt wird nicht, wie bei der Skalarmultiplikation, ein Vektor mit einem Skalar multiplziert, sondern stattdessen ein Vektor mit einem Vektor. Das Ergebnis dieser Rechnung - also das Produkt - ist immer ein Skalar. Daher auch der Name Skalarprodukt.

Das Skalarprodukt wird dazu verwendet, den Winkel zwischen zwei Vektoren auszurechnen. Insbesondere dann, wenn man die Lagebeziehungen untersuchen will, ist die Formel äußerst nützlich und wird häufig verwendet. Durch sie kann man herausfinden, ob Vektoren, Geraden, oder Ebenen senkrecht zueinander liegen (also im 90°-Winkel).

2. Formel

Das Skalarprodukt ist glücklicherweise sehr leicht zu errechnen.



Allgemein:





Beispiel:





Beispiel:

3. Hinweise

• Für die Winkelberechnung später nützlich und wichtig ist folgende Regel:
  
  
  
  
  
  
  Sprich: Das Ergebnis von Vektor a mal Vektor b ist gleich dem Ergebnis aus Betrag von Vektor a mal Betrag von Vektor b mal Cosinus von phi, wobei phi der Winkel zwischen Vektor a und Vektor b ist.
  
• Die Schreibweise 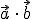ist nicht die einzige verwendete für das Skalarprodukt. Häufig wird auch 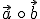, oder 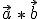benutzt. Nur 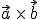steht für eine andere Formel (Kreuzprodukt bzw. Vektorprodukt) und sollte daher nicht mit dem Skalarprodukt verwechselt werden.