auch genannt: inneres Produkt
Beim Skalarprodukt wird nicht, wie bei der Skalarmultiplikation, ein Vektor mit einem Skalar multiplziert, sondern stattdessen ein Vektor mit einem Vektor. Das Ergebnis dieser Rechnung - also das Produkt - ist immer ein Skalar. Daher auch der Name Skalarprodukt.
Das Skalarprodukt wird dazu verwendet, den Winkel zwischen zwei Vektoren auszurechnen. Insbesondere dann, wenn man die Lagebeziehungen untersuchen will, ist die Formel äußerst nützlich und wird häufig verwendet. Durch sie kann man herausfinden, ob Vektoren, Geraden, oder Ebenen senkrecht zueinander liegen (also im 90°-Winkel).
Das Skalarprodukt ist glücklicherweise sehr leicht zu errechnen.
Allgemein:
Beispiel:
Beispiel:
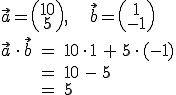
1. Einleitung
Beim Skalarprodukt wird nicht, wie bei der Skalarmultiplikation, ein Vektor mit einem Skalar multiplziert, sondern stattdessen ein Vektor mit einem Vektor. Das Ergebnis dieser Rechnung - also das Produkt - ist immer ein Skalar. Daher auch der Name Skalarprodukt.
Das Skalarprodukt wird dazu verwendet, den Winkel zwischen zwei Vektoren auszurechnen. Insbesondere dann, wenn man die Lagebeziehungen untersuchen will, ist die Formel äußerst nützlich und wird häufig verwendet. Durch sie kann man herausfinden, ob Vektoren, Geraden, oder Ebenen senkrecht zueinander liegen (also im 90°-Winkel).
2. Formel
Das Skalarprodukt ist glücklicherweise sehr leicht zu errechnen.
Allgemein:
Beispiel:
Beispiel:
3. Hinweise
- Für die Winkelberechnung später nützlich und wichtig ist folgende Regel:
Sprich: Das Ergebnis von Vektor a mal Vektor b ist gleich dem Ergebnis aus Betrag von Vektor a mal Betrag von Vektor b mal Cosinus von phi, wobei phi der Winkel zwischen Vektor a und Vektor b ist. - Die Schreibweise
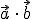ist nicht die einzige verwendete für das Skalarprodukt. Häufig wird auch 
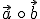, oder 
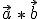benutzt. Nur 
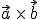steht für eine andere Formel (Kreuzprodukt bzw. Vektorprodukt) und sollte daher nicht mit dem Skalarprodukt verwechselt werden.
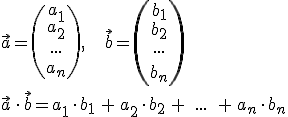
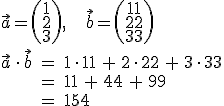
Kommentare (13)
Von neu nach altWir bitten um ihr Verständnis.
Ist das Ergebnis = 0, so sind die Vektoren orthogonal also senkrecht zueinander. Das bedeutet, sie stehen im 90° - Winkel zueinander. Das ist sehr wichtig, denn sonst habe ich ja keine Ahnung, wie ich das errechnete Ergebnis interpretieren soll.
Mir wurds im Mathe LK so erklärt: eine reele Zahl (also im Prinzip ein skalar) ist nur ein Punkt im Raum. Wie man sich sicher denken kann ist ein Punkt keine gerichtete Größe sondern eben nur ein Punkt. Ich hoffe das hilft
Vektor a "skalarmultipliziert" Vektor b
um die Verwechslung mit der einfachen Multiplikation
Vektor a "mal" Vektor b zu vermeiden.
;-)
Klar soweit?
Multipliziert man die Zahlen aus linken Vektorklammer (-> Komponenten) nacheinander mit den Zahlen aus der rechten Vektorklammer und addiert alles zusammen, erhält man das Skalarprodukt.
Anfangen kann man damit alleine nicht viel. Allerdings: wenn das Ergebnis 0 ist, liegen beide Vektoren in einem rechten Winkel zueinander.
Wichtig ist, dass man weiß WIE man ein Skalarprodukt ausrechnet, weil man damit später oft arbeitet (z.B. um den Winkel zwischen zwei Vektoren auszurechnen).
habe eine Frage, wie muss ich die bsp. Aufgaben am Ende weiter rechen, ich meine die Winkelberechnung. Ich bitte von den beiden bsp. Aufgaben nur das eine mit Winkelberchung zu ende zu rechnen, weil ich es nicht ganz verstanden habe, danke!!!
Der Fehler wurde behoben.