Der Name der Skalarmultiplikation ist selbstbeschreibend: Ein Vektor wird mit einem Skalar multipliziert.
Wiederholung: Skalar
Bei der Skalarmultiplikation rechnet man - genauso wie bei der Vektoraddition und -subtraktion - komponentenweise. Man multipliziert also jeweils jede einzelne Komponente des Vektors (in der Schule meist zwei oder drei Komponenten) mit dem Skalar. Als Ergebnis erhält man einen Vektor (im Gegensatz zum Skalarprodukt, wo man einen Skalar als Ergebnis erhält).
Allgemein:
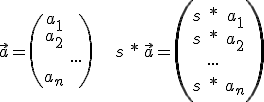
"s" steht hier für einen beliebigen Skalar, z.B. 1 oder auch 10
Beispiel: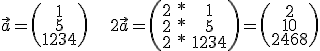
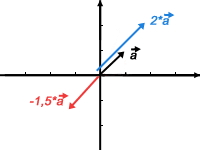
Multipliziert man einen Vektor mit einem Skalar, so verändert man die Länge des Vektors um den Faktor des Skalars. Multipliziert man also bspw. einen Vektor mit 2, so verdoppelt sich dadurch dessen Länge, multipliziert man mit 10, so verzehnfacht sie sich usw.
Die Richtung des Vektors bleibt von der Multiplikation unberührt, es sei denn man verwendet einen negativen Skalar. In diesem Fall entsteht der Gegenvektor - der neue Vektor zeigt also in die genau entgegengesetzte Richtung.
(Vektor a in schwarz, 2*Vektor a in blau, -1,5*Vektor a in rot)
Wiederholung: Skalar
"Skalar" ist ein anderer Name für eine reelle Zahl. Ein Skalar ist also eine ungerichtete Größe - im Gegensatz zu einem Vektor, der eine Richtung besitzt. Temperatur, Länge, oder auch die Zeit sind bspw. Skalare.
Bei der Skalarmultiplikation rechnet man - genauso wie bei der Vektoraddition und -subtraktion - komponentenweise. Man multipliziert also jeweils jede einzelne Komponente des Vektors (in der Schule meist zwei oder drei Komponenten) mit dem Skalar. Als Ergebnis erhält man einen Vektor (im Gegensatz zum Skalarprodukt, wo man einen Skalar als Ergebnis erhält).
1. Formel
Allgemein:
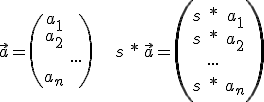
"s" steht hier für einen beliebigen Skalar, z.B. 1 oder auch 10
Beispiel:
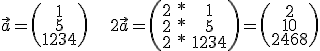
2. geometrische Bedeutung
Multipliziert man einen Vektor mit einem Skalar, so verändert man die Länge des Vektors um den Faktor des Skalars. Multipliziert man also bspw. einen Vektor mit 2, so verdoppelt sich dadurch dessen Länge, multipliziert man mit 10, so verzehnfacht sie sich usw.
Die Richtung des Vektors bleibt von der Multiplikation unberührt, es sei denn man verwendet einen negativen Skalar. In diesem Fall entsteht der Gegenvektor - der neue Vektor zeigt also in die genau entgegengesetzte Richtung.
(Vektor a in schwarz, 2*Vektor a in blau, -1,5*Vektor a in rot)
Kommentare (8)
Von neu nach altWir bitten um ihr Verständnis.
-->> als Ergebnis erhält man ein Skalar (im Gegensatz zu Vektorprodukt, wo man ein Vektor erhält.