1. Einleitung
Zwei Vektoren bezeichnet man immer dann als "orthogonal", wenn sie senkrecht zueinander liegen. Der von ihnen eingeschlossene Winkel muss also 90° sein. Daher auch das Wort orthogonal, welches aus dem griechischen stammt und dort für rechtwinklig steht.
Um herauszufinden, ob zwei Vektoren senkrecht zueinander liegen, muss man allerdings keine langwierige Winkelberechnung durchführen, sondern muss nur überprüfen, ob das Skalarprodukt 0 ergibt. Ist es 0, so bilden die Vektoren einen rechten Winkel.
2. Formel
Allgemein:
Der Winkel zwischen zwei Vektoren
ist immer dann 90°, wenn gilt
.
ist immer dann 90°, wenn gilt
.Beispiel:
3. Begründung
Es gilt die Formel vom Skalarprodukt:
Wenn nun der Winkel
gleich 90° ist, so ist der Cosinus von gleich 0 (Cosinus von 0°=1, Cosinus von 90°=0).Damit würde in diesem Fall gelten
.4. Umkehrung: Einen orthogonalen Vektor finden
Wenn man nachweisen kann, dass ein Vektor zu einem anderen Vektor orthogonal ist, dann kann man diesen Nachweis logischerweise auch umkehren und auf diese Weise herausfinden, welcher Vektor zu einem anderen Vektor orthogonal liegt.
Hierzu muss man nur herausfinden, welcher gesuchte Vektor multipliziert mit dem gegebenen Vektor 0 ergibt.
5. Formel: Umkehrung
Allgemein:
ist ein bekannter Vektor,
ist ein gesuchter Vektor.
Die Formel ist also sehr ähnlich wie die des Skalarprodukts, nur dass
bekannt ist und das Ergebnis 0 sein muss.Beispiel:
bekannter Vektor 
gesuchter Vektor
gesuchter Vektor
Hieraus kann man nun beliebig viele Vektoren bilden, die alle orthogonal zu
sind. Zum Beispiel 
, oder 
, oder 
.Am einfachsten kann man dies errechnen, indem man für einen Wert 0 einsetzt, z.B.
. Dann muss nur noch gelten 
.Man kann natürlich nicht für alle drei Werte 0 einsetzen, denn dann würde gelten
. Dieser Vektor hat keine Länge - und wie könnte ein Vektor ohne Länge rechtwinklig zu einem anderen Vektor liegen?6. Links
Hier zwei beispielhafte Abituraufgaben, die sich mit der Orthogonalität beschäftigen.
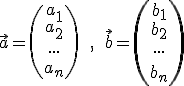
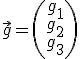
Kommentare (9)
Von neu nach altWir bitten um ihr Verständnis.
identisch sein, da bei beiden ausgerechnet wird,
ob die Vektoren senkrecht zueinander stehen, oder etwa nicht?
Der Nullvektor ist per Definition immer rechtwinklig und parallel zu jedem anderen Vektor. Somit wäre (0,0,0) durchaus eine richtige, wenn auch unbrauchbare Lösung.
bisher fand ich alle artikel echt recht hilfreich... und ich kann wirklich nichts in mathe - ich steh auf der kippe zur 6. -.-
aber irgendwie versteh ich nicht,
wie man am ende dieses artikel auf die neuen g vektoren kommt?