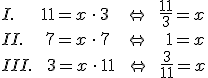1. Einleitung
Die Beschreibungen "lineare Abhängigkeit" und "lineare Unabhängigkeit" erklären, wie Vektoren im Vergleich zu anderen Vektoren ausgerichtet sind. Vektoren können voneinander linear abhängig oder linear unabhängig sein. Schwammig (und ganz unmathematisch!) formuliert, sind voneinander linear abhängige Vektoren untereinander ähnlicher als voneinander linear unabhängige - zumindest wenn man nur die Richtung betrachtet.
2. Mathematisches Vorgehen
Um herauszufinden, ob mehrere Vektoren voneinander linear abhängig sind, kann man sich die Frage stellen, ob sich mindestens einer der Vektoren durch die anderen darstellen lässt. Das heißt, dass man aus einer Menge von mehreren Vektoren einen auswählt; dieser muss sich nun errechnen lassen, indem man alle übrigen Vektoren jeweils mit einem beliebigen Skalar (z.B. 1 oder 10 oder 17,523) multipliziert und dann miteinander addiert.
Mit zwei Vektoren ist dies am leichtesten:
Beispiel 1:
Da sich Vektor a durch Vektor b darstellen lässt, indem man Vektor b mit -0,5 multipliziert, sind beide Vektoren voneinander linear abhängig.
Beispiel 2:
Hier lässt sich Vektor a nicht durch Vektor b darstellen (man kann kein einheitliches x finden). Daher sind Vektor a und Vektor b voneinander linear unabhängig.
Um sich lästige Mehrfachprüfungen zu ersparen (bei mehr als 2 Vektoren) kann man auch einfach alle Vektoren in einer Linearkombination mit 0 gleichsetzen:
Erhält man eine Lösung bei der nicht
bis 
alle gleich 0 sind, also bei der mindestens ein a ungleich 0 ist, so sind die Vektoren voneinander linear abhängig. Erhält man nur die Lösung ...=0, was man auch die "Triviallösung" (trivial=einfach) nennt, so sind die Vektoren voneinander linear unabhängig.3. Merkregeln
) sind drei Vektoren immer voneinander linear abhängig.
) sind vier Vektoren immer voneinander linear abhängig.