Jeder Vektor enthält zwei wichtige Informationen:
Vektoren werden z.B. in der Physik verwendet, um Zugkräfte darzustellen.
Dabei stellt der Vektor die Richtung dar, in die man zieht (=Richtung des Vektors) und die Kraft, die man dafür aufwendet (=Länge des Vektors).
Auch Bewegungen können durch Vektoren dargestellt werden.
In diesem Fall entspräche dann die Vektorrichtung der Bewegungsrichtung und die Vektorlänge der Bewegungsgeschwindigkeit.
Grundsätzlich eignen sich Vektoren für die Darstellung aller Arten von gerichteten Größen.
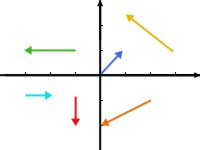
Einige Beispielvektoren im zweidimensionalen Raum:
Achtung: Ein Vektor kann zwar aus Anfangs- und Endpunkt gebildet werden, enthält aber immer nur die beiden Basisinformationen Richtung und Länge.
Man kann also prinzipiell nicht von "dem einen Vektor" sprechen, da man einen Vektorpfeil, über den nur seine Richtung und seine Länge bekannt sind, ja überall im Raum platzieren kann.
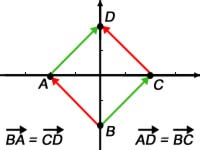
Ein Verbindungsvektor, den man aus einem Anfangspunkt A und einem Endpunkt B errechnet, ergibt also durchaus einen Vektor der unter anderem Punkt A und B durch seine Richtung und seine Länge verbindet.
Dieser Vektor könnte sich aber auch an jeder anderen Position im Raum befinden.
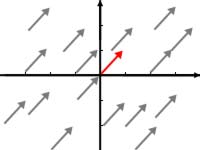
Ein Vektor wird daher auch als "Äquivalenzklasse" bezeichnet.
Man kann nie "den einen" Vektor errechnen, sondern nur eine Klasse.
Innerhalb dieser Klasse gibt es unendlich viele Vektoren, die alle gleich lang sind und in die selbe Richtung zeigen, sich aber an anderen Positionen im Raum befinden.
Diese Tatsache ist nicht nur wichtig, um Pluspunkte beim Mathelehrer zu erhalten, sondern auch später, wenn man Beweise anhand von Vektoren herleiten will (oder muss).
Allgemeine Schreibweise:
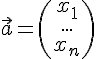
Beispiel:
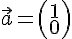
Vektoren werden in Klammern geschrieben mit den einzelnen Koordinatenangaben untereinander und ohne Trennzeichen.
Als Bezeichnung für einen Vektor verwendet man z.B. , oder auch
, oder auch 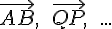 wenn er zwei Punkte verbindet.
wenn er zwei Punkte verbindet.
Der Vektor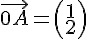 würde z.B. bedeuten: Gehe +1 auf der x1-Achse (im
würde z.B. bedeuten: Gehe +1 auf der x1-Achse (im  gewöhnlich x-Achse), gehe dann +2 auf der x2-Achse (im
gewöhnlich x-Achse), gehe dann +2 auf der x2-Achse (im  gewöhnlich y-Achse).
gewöhnlich y-Achse).
Wie hier auch zu erkennen ist, vewendet man ab der Vektorrechnung als Namen für die Achsen häufig nur noch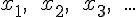 , statt der bis dahin üblichen x,y,z (oder auch u,v,w).
, statt der bis dahin üblichen x,y,z (oder auch u,v,w).
Dies wird insbesondere dann hilfreich, wenn man mit Vektoren, die mehr als drei Dimensionen haben, rechnet.
Der Gegenvektor zu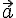 ist derjenige Vektor, der zwar die selbe Länge hat, aber in die genau umgekehrte Richtung zeigt.
ist derjenige Vektor, der zwar die selbe Länge hat, aber in die genau umgekehrte Richtung zeigt.
Dementsprechend ist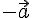 der Gegenvektor zu
der Gegenvektor zu 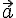 (nach obigen Beispiel ist es nun "Gehe -1 auf der x1-Achse, gehe dann -2 auf der x2-Achse").
(nach obigen Beispiel ist es nun "Gehe -1 auf der x1-Achse, gehe dann -2 auf der x2-Achse").
Den Gegenvektor kann man also schnell bilden indem man ein Minus vor den Vektor setzt.
Bei Vektoren, die zwei Punkte verbinden, kann man auch die beiden Punkte in der Bezeichnung vertauschen:
Auch der Vektor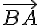 ist der Gegenvektor zu
ist der Gegenvektor zu 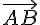 .
.
Der Ortsvektor zu einem Punkt A ist derjenige Vektor, der Ursprung und Punkt A miteinander verbindet, also einfach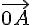 .
.
Dementsprechend ist der Ortsvektor zu B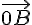 und der Ortsvektor zum Punkt P
und der Ortsvektor zum Punkt P 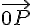 .
.
Der Nullvektor hat die Länge Null.
Einen derartigen Vektor kann man nur dann erhalten, wenn man den Vektor zwischen zwei Punkten berechnet, die identisch sind.
Z.B. hat der Vektor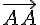 die Länge Null.
die Länge Null.
Einheitsvektoren sind diejenigen Vektoren, die die Länge 1 haben.
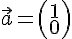 wäre z.B. ein Einheitsvektor.
wäre z.B. ein Einheitsvektor.
- Seine Länge (in Bezug auf Vektoren gewöhnlich als Betrag bezeichnet)
- Eine Richtung
Vektoren werden z.B. in der Physik verwendet, um Zugkräfte darzustellen.
Dabei stellt der Vektor die Richtung dar, in die man zieht (=Richtung des Vektors) und die Kraft, die man dafür aufwendet (=Länge des Vektors).
Auch Bewegungen können durch Vektoren dargestellt werden.
In diesem Fall entspräche dann die Vektorrichtung der Bewegungsrichtung und die Vektorlänge der Bewegungsgeschwindigkeit.
Grundsätzlich eignen sich Vektoren für die Darstellung aller Arten von gerichteten Größen.
Einige Beispielvektoren im zweidimensionalen Raum:
Achtung: Ein Vektor kann zwar aus Anfangs- und Endpunkt gebildet werden, enthält aber immer nur die beiden Basisinformationen Richtung und Länge.
Man kann also prinzipiell nicht von "dem einen Vektor" sprechen, da man einen Vektorpfeil, über den nur seine Richtung und seine Länge bekannt sind, ja überall im Raum platzieren kann.
Ein Verbindungsvektor, den man aus einem Anfangspunkt A und einem Endpunkt B errechnet, ergibt also durchaus einen Vektor der unter anderem Punkt A und B durch seine Richtung und seine Länge verbindet.
Dieser Vektor könnte sich aber auch an jeder anderen Position im Raum befinden.
Ein Vektor wird daher auch als "Äquivalenzklasse" bezeichnet.
Man kann nie "den einen" Vektor errechnen, sondern nur eine Klasse.
Innerhalb dieser Klasse gibt es unendlich viele Vektoren, die alle gleich lang sind und in die selbe Richtung zeigen, sich aber an anderen Positionen im Raum befinden.
Diese Tatsache ist nicht nur wichtig, um Pluspunkte beim Mathelehrer zu erhalten, sondern auch später, wenn man Beweise anhand von Vektoren herleiten will (oder muss).
1. Mathematische Schreibweise von Vektoren
Allgemeine Schreibweise:
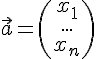
Beispiel:

Vektoren werden in Klammern geschrieben mit den einzelnen Koordinatenangaben untereinander und ohne Trennzeichen.
Als Bezeichnung für einen Vektor verwendet man z.B.
Der Vektor
Wie hier auch zu erkennen ist, vewendet man ab der Vektorrechnung als Namen für die Achsen häufig nur noch
Dies wird insbesondere dann hilfreich, wenn man mit Vektoren, die mehr als drei Dimensionen haben, rechnet.
2. Der Gegenvektor
Der Gegenvektor zu
Dementsprechend ist
Den Gegenvektor kann man also schnell bilden indem man ein Minus vor den Vektor setzt.
Bei Vektoren, die zwei Punkte verbinden, kann man auch die beiden Punkte in der Bezeichnung vertauschen:
Auch der Vektor
3. Der Ortsvektor
Der Ortsvektor zu einem Punkt A ist derjenige Vektor, der Ursprung und Punkt A miteinander verbindet, also einfach
Dementsprechend ist der Ortsvektor zu B
4. Der Nullvektor
Der Nullvektor hat die Länge Null.
Einen derartigen Vektor kann man nur dann erhalten, wenn man den Vektor zwischen zwei Punkten berechnet, die identisch sind.
Z.B. hat der Vektor
5. Der Einheitsvektor
Einheitsvektoren sind diejenigen Vektoren, die die Länge 1 haben.
Kommentare (5)
Von neu nach altWir bitten um ihr Verständnis.
Könnte der Betreiber ja mal ändern nach 2 Jahren
Dargestellt in dem Diagramm ist der Ortsvektor für den Punkt (1,1) und wie man in der Def. für Ortsvektoren oben sehen kann, wäre das (1/1).
Beispiel: a=(1/0) stimmt mit dem nebenstehenden Diagramm (1/1) nicht überein.
Ansonst sehr gut erklärt.