1. Einleitung
Es gibt insgesamt vier Arten wie Geraden zueinander liegen können:
- Windschief: Geraden sind nicht parallel und haben keinen Schnittpunkt.
- Parallel: Sind parallel, haben aber keinen Schnittpunkt.
- Identisch: Sie liegen "ineinander", es lässt sich hier kein eindeutiger Schnittpunkt bestimmen.
- Schneiden: Die Geraden schneiden sich an genau einem Punkt.
Wie man leicht erkennen kann, gibt es also nur einen Fall bei dem man einen Schnittpunkt erhält. Es gibt allerdings keine Möglichkeit vorher leicht zu überprüfen, ob sich die Geraden an nur einem Punkt schneiden. Man kann nur einen Teil der anderen Fälle ausschließen.
Denn sind die Richtungsvektoren der beiden Geraden nicht linear abhängig, dann können die Geraden schonmal nicht parallel und nicht identisch sein. Sind die Richtungsvektoren aber linear abhängig, dann können die Geraden nicht windschief sein und sich nicht schneiden.
Es empfiehlt sich also vor dem Rechnen erstmal zu schauen, ob die Richtungsvektoren der Geraden voneinander linear abhängig sind. Wenn ja, dann lässt sich kein eindeutiger Schnittpunkt bestimmen (Geraden sind identisch) oder es gibt keinen Schnittpunkt (Geraden sind parallel). Wenn die Richtungsvektoren nicht linear abhängig sind, dann kommt man aber nicht ums Rechnen herum.
2. Vorgehen
Um den Schnittpunkt zu bestimmen geht man wie folgt vor:
- Prüfen: Sind die Richtungsvektoren linear abhängig?
- Wenn nein: Geraden gleichsetzen (also eine Geradengleichung für
der anderen Geradengleichung einsetzen)
- Das ergibt ein lineares Gleichungssystem. Beide Variablen ausrechnen (
und
). In die dritte Gleichung einsetzen (Test). Bei wahrem Ergebnis (z.B. 1=1) gibt es einen Schnittpunkt, bei unwahrem Ergebnis sind die Geraden windschief.
- Das Ergebnis für diese Variable bei der entsprechenden Geradengleichung einsetzen.
- Ausrechnen, das Ergebnis ist der Schnittpunkt.
Beispiel:
Gegeben:
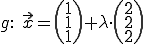
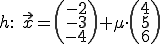
Wichtig: Falls die beiden Variablen vor den Richtungsvektoren in der Aufgabe die selben sind, dann muss man sie ändern, sodass man zwei verschiedene hat. Sonst bekommt man ab dem linearen Gleichungssystem nur noch Mist heraus! (Hier sind die Variablen schon verschieden: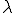 und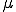
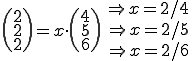
Offensichtlich lässt sich kein einheitliches x finden, daher sind die Vektoren linear unabhängig.
Geraden werden gleichgesetzt:
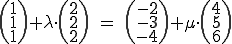
Das ganze wandelt man jetzt einfach in ein lineares Gleichungssystem um:
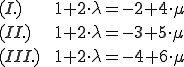
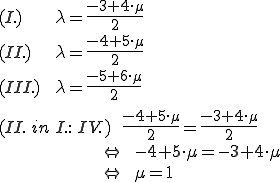
Eigentlich ist das (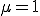
) jetzt schon das Ergebnis.
Leider muss man aber noch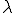 (Lambda) ausrechen und dann beide Variablen in die dritte Gleichung einsetzen. Erst wenn dann ein wahres Ergebnis herauskommt kann man sich sicher sein, dass das Ergebnis stimmt.
Würde man das nicht tun, dann könnte es nämlich sein, dass man zwei windschiefe Geraden hat. In diesem Fall kann man ohne Probleme für eine Variable einen Wert erhalten. Dass das Ergebnis dann aber falsch ist, erkennt man, wenn man zwei Variablen in eine Gleichung einsetzt - dann kommt ein unwahres Ergebnis heraus!
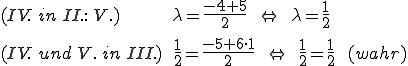
Das Ergebnis ist wahr, die Geraden schneiden also. Jetzt muss nur noch der Schnittpunkt errechnet werden.
Dazu wird eine der Variablen in die jeweils zugehörige Geradengleichung eingesetzt - also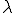 in "g" oder 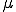in "h". Wir wählen mal 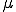in h, denn 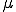= 1 ist schön einfach zu rechnen.
(S ist der Schnittpunkt,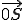
der Vektor, der auf den Schnittpunkt zeigt.)
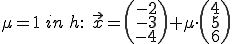
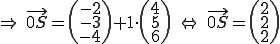
Der Schnittpunkt der beiden Geraden ist also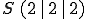
.
Wichtig: Falls die beiden Variablen vor den Richtungsvektoren in der Aufgabe die selben sind, dann muss man sie ändern, sodass man zwei verschiedene hat. Sonst bekommt man ab dem linearen Gleichungssystem nur noch Mist heraus! (Hier sind die Variablen schon verschieden:
Offensichtlich lässt sich kein einheitliches x finden, daher sind die Vektoren linear unabhängig.
Geraden werden gleichgesetzt:
Das ganze wandelt man jetzt einfach in ein lineares Gleichungssystem um:
Eigentlich ist das (
Leider muss man aber noch
Würde man das nicht tun, dann könnte es nämlich sein, dass man zwei windschiefe Geraden hat. In diesem Fall kann man ohne Probleme für eine Variable einen Wert erhalten. Dass das Ergebnis dann aber falsch ist, erkennt man, wenn man zwei Variablen in eine Gleichung einsetzt - dann kommt ein unwahres Ergebnis heraus!
Das Ergebnis ist wahr, die Geraden schneiden also. Jetzt muss nur noch der Schnittpunkt errechnet werden.
Dazu wird eine der Variablen in die jeweils zugehörige Geradengleichung eingesetzt - also
(S ist der Schnittpunkt,
Der Schnittpunkt der beiden Geraden ist also
Kommentare (8)
Von neu nach altWir bitten um ihr Verständnis.
wenn die Richtungsverktoren linear abhängig sind, solltet ihr noch schauen, ob der Stützverktor auf der anderen Gereade liegt, weil dann sind sie identisch.
Dies wurde hier nicht erwähnt.
Ansonsten alles super.