1. Einleitung
Es gibt 3 mögliche Arten, wie Geraden und Ebenen zueinander liegen können. Aber nur bei in einem Fall gibt es einen richtigen Schnittpunkt:
- Gerade schneidet Ebene: Hier gibt es einen Schnittpunkt.
- Gerade liegt in Ebene: Hier gibt es keinen "richtigen" Schnittpunkt - sondern unendlich viele! Die ganze Gerade liegt in der Ebene, daher sind alle Punkte auf der Geraden Schnittpunkte.
- Gerade parallel zur Ebene: Kein einziger Schnittpunkt.
Um herauszufinden, welcher dieser drei Fälle vorliegt kann man den Richtungsvektor der Geraden und den Normalenvektor der Ebene miteinander vergleichen. Danach müsste man auch noch einen Punkt der Geraden in die Ebene einsetzen.
Das tut man aber nicht, denn das dauert schon fast genauso lange wie einfach direkt die Rechnung auszuführen (und wenn man herausfindet, dass ein Schnittpunkt vorliegt, dann muss man sowieso rechnen).
Praktischerweise spiegeln sich auch alle drei möglichen Lagebeziehungen zwischen Ebene und Gerade im Ergebnis der Rechnung wieder. Für jeden der drei Fälle bekommt man also ein typisches Ergebnis heraus durch das man sofort erkennen kann, welcher Fall vorliegt.
Zuersteinmal aber das grundsätzliche Vorgehen (also wie man beginnt):
Man benötigt neben der gegebenen Geraden auch eine Ebene. Die Ebene sollte in Koordinatenform gegeben sein. Ist sie das nicht, dann muss man sie dahin umrechnen, denn nur mit der Koordinatenform geht die Rechnung sehr einfach. Danach setzt man die Gerade einfach in die Ebenengleichung ein.
Wenn man das jetzt ausrechnet (nach dem Einsetzen), dann kommt man am Ende wieder auf die drei oben genannten Fälle zurück. Zuletzt muss dort nämlich irgendwas stehen in der Art ...=..., woraus man ableiten kann, ob es einen Schnittpunkt gibt, unendlich viele, oder gar keine:
- Variable=Wert: z.B.
. Bekommt man ein Ergebnis mit einer Variablen und einem Wert für diese Variable heraus, dann liegt ein Schnittpunkt vor.
- x=x (wahres Ergebnis): z.B. 1=1, oder 17=17, oder 100=100. Ist das Ergebnis wahr, dann liegen unendlich viele Schnittpunkte vor. Die Gerade liegt also in der Ebene.
- x=y (unwahres Ergebnis): z.B. 1=2, oder 0=1, oder 12983=10. Ist das Ergebnis unwahr, dann gibt es keinen Schnittpunkt. Die Gerade und die Ebene liegen also parallel.
2. Beispiel: Gerade schneidet Ebene
Merkmale: Genau ein Schnittpunkt, das Ergebnis muss im Format Variable=Wert sein.
Gegeben:
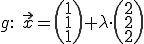
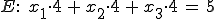
g wird in E eingesetzt:
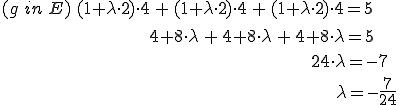
Es ist also ein Wert im Format Variable=Wert herausgekommen, es gibt also tatsächlich einen Schnittpunkt. Jetzt muss nur noch dieser Wert für die Variable in der Geradengleichung eingesetzt werden:
(S: Der Schnittpunkt)
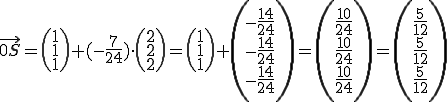
Der Schnittpunkt von Gerade und Ebene liegt also bei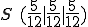 .
.
g wird in E eingesetzt:
Es ist also ein Wert im Format Variable=Wert herausgekommen, es gibt also tatsächlich einen Schnittpunkt. Jetzt muss nur noch dieser Wert für die Variable in der Geradengleichung eingesetzt werden:
(S: Der Schnittpunkt)
Der Schnittpunkt von Gerade und Ebene liegt also bei
3. Beispiel: Gerade liegt in Ebene
Merkmale: Unendlich viele Schnittpunkte, das Ergebnis hat das Format x=x (wahre Aussage, z.B. 1=1 oder 7=7).
Gegeben:
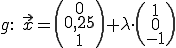
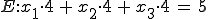
g wird in E eingesetzt:
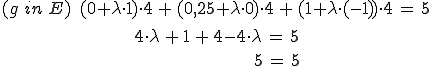
5 = 5 ist das Ergebnis, das zu den Merkmalen (weiter oben) passt. Damit braucht man auch nicht mehr weiterzurechnen, denn die Gerade liegt genau in der Ebene. Will man die Schnittpunkte angeben (unendlich viele), dann kann man dazu einfach die Geradengleichung verwenden, denn alle Schnittpunkte liegen auf der Gerade.
g wird in E eingesetzt:
5 = 5 ist das Ergebnis, das zu den Merkmalen (weiter oben) passt. Damit braucht man auch nicht mehr weiterzurechnen, denn die Gerade liegt genau in der Ebene. Will man die Schnittpunkte angeben (unendlich viele), dann kann man dazu einfach die Geradengleichung verwenden, denn alle Schnittpunkte liegen auf der Gerade.
4. Beispiel: Gerade liegt parallel zur Ebene
Merkmale: Kein Schnittpunkt, das Ergebnis hat das Format x=y (unwahre Aussage, z.B. 1=2, oder 100=-100, oder 5=9873).
Gegeben:
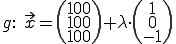
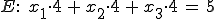
g wird in E eingesetzt:
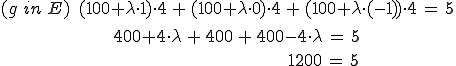
Das Ergebnis ist unwahr und daher muss nicht weitergerechnet werden. Die Gerade und die Ebene müssen parallel sein (sonst würden sie mindestens einen Schnittpunkt haben).
g wird in E eingesetzt:
Das Ergebnis ist unwahr und daher muss nicht weitergerechnet werden. Die Gerade und die Ebene müssen parallel sein (sonst würden sie mindestens einen Schnittpunkt haben).
Kommentare (37)
Von neu nach altWir bitten um ihr Verständnis.
Ohne großes Bling-Bling oder Gerede, alle Fakten auf einmal. Optimal wenn man sich unsicher ist etc und eine spezifische Frage hat.
Manchmal frage ich mich wieso es noch Lehrer gibt, wenn sie zu inkompetent sind einem etwas richtig beizubringen.
Hiermit klappt es viel kompakter und zielorientierter!
LOB!