1. Einleitung
Es gibt bei Ebenen drei Fälle wie sie zueinander liegen können:
- Sie liegen parallel: Es gibt keinen einzigen Schnittpunkt.
- Sie liegen ineinander: Es gibt unendlich viele Schnittpunkte.
- Sie schneiden einander: Es gibt ebenfalls unendlich viele Schnittpunkte. Diese liegen aber alle auf einer sogenannten Schnittgeraden, die genau an der Stelle liegt, an der sich die beiden Ebenen schneiden.
Die Rechnung für die Schnittgerade ist leider etwas komplexer. Daher empfiehlt es sich, vorher ersteinmal zu überprüfen, ob sich die Geraden überhaupt schneiden. Sofern die Ebenen in Koordinatenform gegeben sind ist das nicht sonderlich schwer. Sind sie nicht in Koordinatenform gegeben, dann muss man sie umrechnen (das muss man für die Berechnung der Schnittgeraden aber sowieso).
Die Überprüfung, wie die Ebenen zueinander liegen, erfolgt in einigen kurzen Schritten:
- Prüfen: Sind die Normalenvektoren der beiden Ebenen voneinander linear abhängig?
- Wenn nein (nicht linear abhängig): Die Ebenen schneiden auf jeden Fall.
- Wenn ja (linear abhängig): Die Ebenen sind mindestens parallel.
- Prüfen: Liegt ein (beliebig gewählter) Punkt von einer der beiden Ebenen in der anderen Ebene?
- Wenn nein (Punkt liegt nicht in Ebene): Ebenen sind nur parallel.
- Wenn ja (Punkt liegt in Ebene): Die Ebenen liegen ineinander.
Also: Nur dann, wenn die beiden Normalenvektoren linear unabhängig sind, muss man die Schnittgerade ausrechnen.
2. Berechnung Schnittgerade
Zu Anfang des Rechnungsweges hat man erstmal nur die beiden Ebenengleichungen in Koordinantenform. Aus diesen muss man ein lineares Gleichungssystem, bei dem einfach die erste Bedingung die Ebenengleichung der ersten Ebene ist und entsprechend die zweite Bedingung die Ebenengleichung der zweiten Ebene. Das ganze könnte dann z.B. so aussehen:
Aus einer der beiden Gleichungen (z.B. II) muss man dann irgendwie eines der drei "x" rauswerfen (z.B. x1). Es bleiben danach zwei der drei x in der Gleichung stehen. Für eines dieser beiden x setzt man dann eine Variable ein, z.B.
Beispiel (nicht nachgerechnet):
Die Werte für x2 und x3 setzt man dann in diejenige der beiden Ebenengleichung ein, die am Anfang nicht weiterverwendet wurde (um die Variablen zu erhalten). Im Beispiel wäre das also Gleichung I. Man erhält dann einen Wert für x1. Die Werte für x1, x2 und x3 kann man nun einfach in einen einzigen Vektor schreiben. Stellt man diese richtig um, dann ergibt sich eine Geradengleichung.
Beispiel (nicht nachgerechnet):
3. Beispiel: Ebenen schneiden
Gegeben:
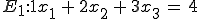
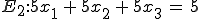
Normalenvektor finden und lineare Abhängigkeit prüfen:
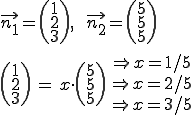
Es lässt sich kein einheitliches x finden, daher müssen die beiden Normalenvektoren linear unabhängig sein.
Da sie linear unabhängig sind, müssen sich auch die Ebenen schneiden und es muss eine Schnittgerade errechnet werden:
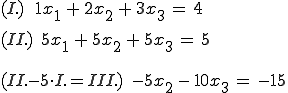
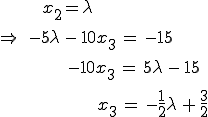
x2 und x3 sind damit gefunden, nun müssen die Werte für beide Variablen in die erste Gleichung eingesetzt werden, sodass man x1 findet:
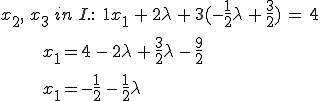
Aus x1, x2 und x3 formt man nun einfach eine Geradengleichung:
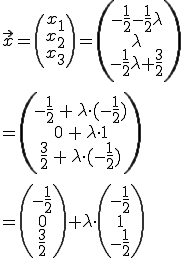
Die Schnittgerade lautet also wie folgt:
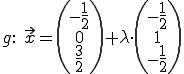
Normalenvektor finden und lineare Abhängigkeit prüfen:
Es lässt sich kein einheitliches x finden, daher müssen die beiden Normalenvektoren linear unabhängig sein.
Da sie linear unabhängig sind, müssen sich auch die Ebenen schneiden und es muss eine Schnittgerade errechnet werden:
x2 und x3 sind damit gefunden, nun müssen die Werte für beide Variablen in die erste Gleichung eingesetzt werden, sodass man x1 findet:
Aus x1, x2 und x3 formt man nun einfach eine Geradengleichung:
Die Schnittgerade lautet also wie folgt:
Kommentare (19)
Von neu nach altWir bitten um ihr Verständnis.
Die Gleichungen (I) und (II) werden miteinander nicht "verbunden". Du streichst das x1 der Gleichung (II) weg und errechnest ohne Gleichung (I) einzubeziehen die Werte x2 und x3.
Zweiter Teil der Rechnung ist korrekt.
- Wenn ja [...]: Die Ebenen sind mindestens parallel."
Wieso mindestens ? Was wäre den die andere Möglichkeit ?
"Die Werte für x2 und x3 setzt man dann in diejenige der beiden Ebenengleichung ein, die am Anfang nicht weiterverwendet wurde (um die Variablen zu erhalten)."
Es werden sowieso beide Ebenen Gleichungen verwendet. Daher ist es egal, in welche nun später eingesetzt wird.
Bei deiner oberen Berechnung der Schnittgeraden ( ich weiß da steht nicht nachgerechnet aber es ist ein sehr grober Fehler der zu Unschlüsigkeit und nicht-Verständnis führen kann ) "schmeißt" du zwar das x1 raus, subtrahierst dabei aber nicht im x2 / x3 Wert genauso wenig wie den rechten Teil der Gleichung. Im unteren Teil ist dieser Schritt korrekt ausgeführt, im oberen aber nicht. Zum besseren Verständnis für Leute die diesen Beitrag zum grundlegenden Verständnis heranziehen finde ich das daher wichtig es zu ändern.
Ansonsten ein sehr gelungener und hilfreicher Beitrag, hat mich wieder vollkommen fit gemacht in diesem Gebiet!!
LG
Oben bei: "Die Rechnung für die Schnittgerade ist leider etwas komplexer. Daher empfiehlt es sich, vorher ersteinmal zu überprüfen, ob sich die Geraden überhaupt schneiden." -müsste das nicht heißen "[....] Daher empfiehlt es sich, vorher zu überprüfen, ob sich die Ebenen überhaupt schneiden" ? Falls nicht löscht diesen post oder kommentiert diesen. Danke im vorraus.
mfg Fredi