1. Einleitung
In diesem Artikel wird erläutert, wie die Lagebeziehungen zweier Geraden im Raum sein können. Dazu werden zunächst die verschiedenen Möglichkeiten genannt, wie Geraden im Vergleich zueinander im Raum liegen können. Danach folgen Erklärungen, was diese Möglichkeiten auszeichnet und wie man sie anhand der Geradengleichungen erkennen kann.
2. Die vier verschiedenen Möglichkeiten
Die verschiedenen Lagebeziehungen von Geraden zu erkennen und zu verstehen ist nicht sonderlich schwer. Das ändert aber nichts daran, dass sie für die Vektorrechnung äußerst wichtig sind und immer wieder vorkommen. Daher sollte man sie unbedingt verstehen und erkennen können!
Es gibt vier verschiedene Möglichkeiten, wie Geraden zueinander liegen können:
- Die Geraden sind identisch. Sie liegen sozusagen "ineinander" und zeigen daher auf genau die selben Punkte im Raum.
- Die Geraden sind parallel.
- Geraden schneiden sich. Hier lässt sich ein Schnittpunkt berechnen.
- Die Geraden sind windschief. Komischer Name, heißt aber wirklich so. Das bedeuted nichts anderes, als dass sich die Geraden nie schneiden, aber auch nicht parallel sind.
Anmerkung: Im zweidimensionalen Raum gibt es keine windschiefen Geraden und daher nur drei Möglichkeiten!
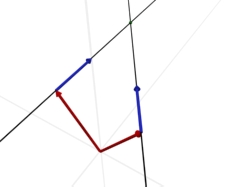
3. Die Geraden sind identisch
Wenn man sagt, dass zwei Geraden "identisch" sind, dann meint man nichts anderes, als dass sie auf genau die selben Punkte zeigen. Der einfachste Fall unter identischen Geraden ist - logischerweise - dass die Geraden genau identisch sind, also der Stützvektor und der Richtungsvektor bei beiden Geraden exakt gleich ist. Aber es gibt auch etwas schwierigere Fälle:
In diesem Fall sind Stützvektor und Richtungsvektor jeweils verschieden. Trotzdem bildet sich aber in beiden Fällen die selbe Gerade. Das liegt daran, dass zum einen die Richtungsvektoren in die selbe Richtung zeigen und nur unterschiedlich lang sind. Zum anderen daran, dass die Stützvektoren von beiden Geraden auf der jeweils anderen Geraden liegen. Ob zwei Geraden also identisch sind, erkennt man indem man
- 1. prüft, ob beide Richtungsvektoren linear abhängig sind.
- 2. prüft, ob einer der beiden Stützvektoren auf der anderen Geraden liegt.
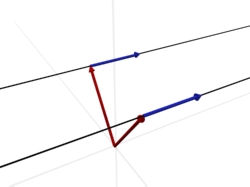
4. Die Geraden sind parallel
Zwei Geraden sind parallel, wenn sie in die gleiche Richtung zeigen, aber nicht identisch sind.
Um herauszufinden, ob zwei Geraden parallel verlaufen, kann man ähnlich vorgehen, wie bei identischen Geraden. In diesem Fall muss bei beiden Geraden die Richtung gleich sein, aber es darf kein Punkt der einen Geraden auf der anderen liegen. Das heißt, dass auch der Stützvektor einer der Geraden nicht auf der anderen liegen darf. Man prüft also
- 1. ob beide Richtungsvektoren linear abhängig sind.
- 2. ob einer der beiden Stützvektoren nicht auf der anderen Geraden liegt.
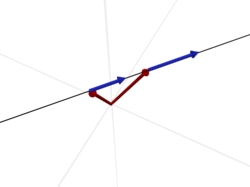
5. Die Geraden schneiden sich
Zwei Geraden schneiden sich, wenn sie genau einen Schnittpunkt haben (wenn sie identisch sind, dann sind es unendlich viele).
Es gibt keinen einfachen Weg, um zu überprüfen, ob sich zwei Geraden schneiden. Man kann nur ausschließen, dass sie parallel oder identisch sind. Danach muss man zwangsweise rechnen und so zu überprüfen, ob man einen Schnittpunkt erhält oder nicht(siehe auch: Geraden sind windschief).
6. Die Geraden sind windschief
Wenn man bei der Überprüfung keinen Schnittpunkt erhält und die Geraden weder identisch noch parallel sind, dann nennt man sie windschief. Der Name klingt etwas komisch, man nennt sie aber wirklich so. Windschiefe Geraden gibt es nicht im zweidimensionalen Raum. Sind im zweidimensionalen Raum die Geraden nicht parallel und nicht identisch, dann schneiden sie immer. Im dreidimensionalen Raum aber müssen sie nicht schneiden.
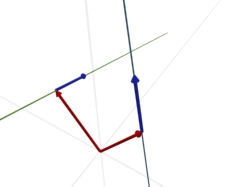
Nicht sofort zu erkennen:
Hier zeigt die vordere Gerade nach "oben", die hintere "in die Ferne".
Die beiden Geraden werden sich nie berühren.
Es gibt keinen einfachen Weg, um zu überprüfen, ob sich zwei Geraden windschief sind. Man kann nur ausschließen, dass sie parallel oder identisch sind. Danach muss man zwangsweise rechnen und so zu überprüfen, ob man einen Schnittpunkt erhält oder nicht (siehe auch: Geraden schneiden sich). Wenn man keinen Schnittpunkt erhält, dann sind die Geraden windschief.
7. Links
Noch einige Videos zum Thema, die auch Beispielrechnungen enthalten:
- (Echt) parallele Geraden
- Sich schneidende Geraden (Schnittprobleme werden auch hier auf rither.de erläutert, aber etwas später)
- Windschiefe Geraden
- Identische Geraden
Kommentare (28)
Von neu nach altWir bitten um ihr Verständnis.
übersichtlich, imformativ und hilft einem super in Mathe Leistung weiter !!!!!!
vielen vielen Dank du hättest Lehrer werden sollen !!!
LG Jonas
Post von Sams83 durchlesen
Schnittlage:
Bedingung 1: Richtungsvektoren sind linear unabhängig.
Bedingung 2: Die Richtungsvektoren und ein weiterer Vektor, von einem Punkt auf der einen Gerade zu einem anderen Punkt auf der anderen Gerade, sind linear abhängig.
(Berechnung der linearen Abhängigkeit dreier Vektoren mit der Determinanten)
Windschiefe Lage:
Bedingung 1: Richtungsvektoren sind linear unabhängig.
Bedingung 2: Die Richtungsvektoren und ein weiterer Vektor, von einem Punkt auf der einen Gerade zu einem anderen Punkt auf der anderen Gerade, sind linear UNabhängig.
Es mag sich für wahrscheinlich auf den ersten Blick komplizierter anhören, wenn man die Determinantenrechnung beherrscht ist es aber viel einfacher.
Hoffe ich konnte euch helfen,
Peace - Dr. Pee
Ich wollte was sagen ... hab's aber vergessen. :D
Super Seite, hilft sehr.
Einfach und verständlich, so wie mans braucht =)