Lage Gerade, Ebene (Thema: Vektorrechnung)

1. Einleitung

In diesem Artikel wird erläutert, wie die Lagebeziehungen einer Geraden und einer Ebene im Vergleich zueinander im Raum sein können. Dazu wird zunächst aufgezählt, welche verschiedenen Lagebeziehungen es gibt. Danach folgen Erklärungen, was diese auszeichnet und wie man sie anhand der Ebenen- und Geradengleichungen erkennen kann.



Hinweis: Die Lagebeziehungen zwischen Geraden und Ebenen sind nicht ganz so wichtig wie bei Gerade/Gerade oder Ebene/Ebene und werden auch nicht so häufig besprochen bzw. in Büchern erwähnt. Trotzdem ist es hilfreich, sie zu beherrschen. So kann man sich einfacher ein Bild davon machen, was man eigentlich an manchen Stellen errechnet.

2. Die drei Möglichkeiten

Wie bei den Lagebeziehungen zwischen zwei Ebenen gibt es auch hier nur drei mögliche Lagen. Das liegt auch hier an der Ebene durch die sich Gerade und Ebene zwangsweise schneiden, wenn sie nicht parallel oder ineinander sind. Aber erstmal zu den Möglichkeiten:

• Gerade liegt in der Ebene. Selbsterklärend: Alle Punkte der Geraden liegen in der Ebene.
• Gerade liegt parallel zur Ebene. Auch selbsterklärend. Hier gibt es keinen einzigen Schnittpunkt.
• Gerade schneidet Ebene. Hier gibt es nur einen einzigen Schnittpunkt.

Die Möglichkeit, dass Gerade und Ebene windschief zueinander liegen, gibt es also auch hier nicht (genauso wie bei zwei Ebenen).

3. Gerade liegt in der Ebene

Alle Punkte, die auf der Geraden liegen, liegen auch in der Ebene.



Das heißt, dass die Gerade jeden ihrer Punkte mit der Ebene "teilt". Es gibt keinen Punkt auf der Geraden, der nicht auch in der Ebene liegt. Daher gibt es unendlich viele Schnittpunkte gibt.

Es ist nicht schwer zu erkennen, ob eine Gerade in einer Ebene liegt - zumindest wenn man den Normalenvektor hat. Andernfalls empfiehlt es sich, diesen zu errechnen. Verfügt man über den Normalenvektor, dann muss man folgende zwei Bedingungen zutreffen:

• 1. Der Richtungsvektor der Geraden muss orthogonal zum Normalenvektor liegen.
• 2. Ein Punkt der Gerade muss in der Ebene liegen.

Gilt eine der beiden Bedinungen nicht, dann liegt die Gerade entweder parallel zur Ebene (Bedingung 1 gilt, 2 aber nicht), oder sie schneidet die Ebene (Bedingung 1 gilt nicht, Bedingung 2 gilt).

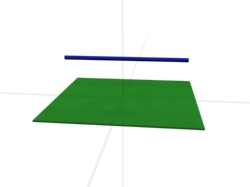
4. Gerade liegt parallel zur Ebene

Wenn die Gerade nicht in der Ebene liegt, sie aber auch niemals schneidet, dann liegt sie parallel zur Ebene.



Um die Frage zu klären, ob Parallelität vorliegt, kann man die obigen zwei Bedingungen nahezu identisch übernehmen. Anders ist nur, dass hier ein Punkt nicht in der Ebene liegen darf (gilt dies für einen Punkt, dann gilt es für alle durch Bedingung 1):

• 1. Der Richtungsvektor der Geraden muss orthogonal zum Normalenvektor liegen.
• 2. Ein Punkt der Gerade darf nicht in der Ebene liegen. (Liegt ein Punkt der Geraden nicht in der Ebene, dann liegt auch kein anderer Punkt in der Ebene.)

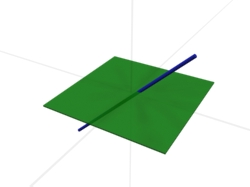
5. Gerade schneidet Ebene

Eine Gerade schneidet eine Ebene, wenn nur ein Schnittpunkt existiert.



Damit sich Ebene und Gerade schneiden müssen sie "schief" zueinander liegen. Ist das der Fall, dann müssen sie sich zwangsweise an irgendeinem Punkt schneiden - und nach diesem Punkt nie wieder.

Die Gerade liegt "schief" zur Ebene, wenn ihr Richtungsvektor nicht orthogonal zum Normalenvektor der Ebene ist. Das heißt, dass Bedingung 1 aus den oberen beiden Fällen sozusagen "umgedreht" wird:

• 1. Der Richtungsvektor der Geraden darf nicht nicht orthogonal zum Normalenvektor liegen.

Hier braucht man auch nur eine Bedingung. Es gibt schließlich nur drei mögliche Lagebeziehungen. Trifft diese Bedingung 1 zu, dann werden automatisch die beiden anderen Fälle (parallel/ineinander) ausgeschlossen. Daher kann nur noch Fall 3 (schneiden) zutreffen.

6. Links

Wiedermal einige Videos, die das ganze etwas verdeutlichen sollen. Vor allem wie man's dann rechnet:

• Ebene in Parameterform und Gerade gegeben - wie liegen sie zueinander?
• Ebene in Normalenform und Gerade gegeben. Wieder die Frage, wie diese zueinander liegen.
• Und das ganze noch einmal, diesmal mit einer Geraden und einer Ebene in Koordinatenform.