1. Einleitung
In diesem Artikel wird erläutert, wie die Lagebeziehungen zweier Ebenen im Raum sein können. Dazu wird zunächst aufgezählt, welche verschiedenen Lagebeziehungen es gibt. Danach folgen Erklärungen, was diese auszeichnet und wie man sie anhand der Ebenengleichungen erkennen kann.
2. Die drei verschiedenen Möglichkeiten
Die verschiedenen Lagebeziehungen zwischen zwei Ebenen zu verstehen ist ähnlich wichtig wie bei zwei Geraden im Raum. Die Lage zweier Ebenen zueinander muss man immer wieder in Aufgaben überprüfen - und teilweise kann man sich so auch viel unnötige Rechenzeit sparen.
Genauso wie bei Geraden im zweidimensionalen Raum, gibt es bei Ebenen im dreidimensionalen Raum nur drei Möglichkeiten, wie sie zueinander liegen können:
- Ebenen sind identisch. Man sagt auch: Sie beschreiben die selben Punkte. Das heißt, dass sie "ineinander" liegen. Die Ebenengleichungen müssen nicht zwangsweise genau gleich sein.
- Ebenen sind parallel. Ziemlich selbsterklärend. Die Ebenen schneiden sich niemals, sind aber auch nicht identisch.
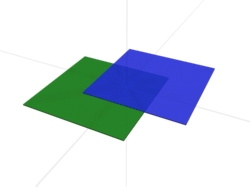
- Ebenen schneiden. In diesem Fall bildet sich eine Schnittgerade an der Stelle, an der sich die beiden Ebenen schneiden.
Im Unterschied zu zwei Geraden im (dreidimensionalen) Raum gibt es also keine windschiefen Ebenen. Das heißt, wenn Ebenen nicht identisch oder parallel sind, dann schneiden sie sich immer!
Hinweis: Wie Ebenen im Vergleich zueinander liegen, ist unterschiedlich schwer zu untersuchen. Mit der Parameterform ist es am schwierigsten, denn hier muss man 4 Richtungsvektoren miteinander vergleichen (2 Ebenen mit jeweils 2 Richtungsvektoren), wenn man herausfinden will, ob die Ebenen parallel verlaufen. Das geht mit der Koordinatenform/Normalenform viel einfacher, da man hier nur zwei Vektoren (die Normalenvektoren) überprüfen muss. Daher wird hier die Koordinatenform verwendet.
3. Ebenen sind identisch
Zwei Ebenen sind dann identisch, wenn beide genau die selben Punkte enthalten. Man kann auch sagen, dass sie "ineinander" liegen.
Zwei identische Ebenen.
(Ausschnitte der Ebenen - eigentlich müssten sie unendlich groß sein.)
Ebenen sind dann automatisch identisch, wenn ihre Ebenengleichung gleich ist. Das muss aber nicht zwangsweise sein. Stellt man die Ebene z.B. mit Hilfe des Normalenvektors dar (Koordinatenform/Normalenform), dann kann man für den Normalenvektor verschiedene Längen verwenden - die Ebene bleibt aber gleich, da sich die Richtung des Normalenvektors nicht verändert.
Bei der Koordinatenform/Normalenform kann man erkennen, ob zwei Ebenen identisch sind, indem man prüft, ...
- 1. ... ob beide Normalenvektoren linear abhängig sind.
- 2. ... ob ein Punkt der einen Ebene in der anderen liegt (gilt es für einen Punkt, dann gilt es durch Bedingung 1 auch für alle anderen) .
4. Ebenen sind parallel
Was Parallelität ist, ist wohl allgemein bekannt. Zwei Ebenen sind parallel wenn sie im Raum gleich "ausgerichtet" sind, aber keine Ebene auch nur einen Punkt der anderen enthält - also wenn sie nicht identisch sind, sich aber auch niemals schneiden.
Die Überprüfung, ob zwei Ebenen parallel sind, ist sehr ähnlich zu der Überprüfung, ob zwei Ebenen identisch sind. Bei Prüfung auf Parallelität schaut man, ...
- 1. ... ob beide Normalenvektoren linear abhängig sind.
- 2. ... ob ein Punkt der einen Ebene nicht in der anderen liegt (gilt es für einen Punkt, dann gilt es durch Bedingung 1 auch für alle anderen) .
5. Ebenen schneiden
Sind zwei Ebenen weder identisch noch parallel, dann schneiden sie sich immer. Sobald sich Ebenen schneiden bildet sich nicht - wie bei Geraden - ein einzelner Schnittpunkt, sondern stattdessen eine Schnittgerade. Das heißt, dass diese unendlich vielen Schnittpunkte alle so liegen, dass sie mit Hilfe einer Geradengleichung beschrieben werden können.
An der Stelle, an der sich die Ebenen schneiden
bildet sich eine Schnittgerade.
Die Überprüfung darauf, ob sich die Ebenen schneiden, ist äußerst leicht. Es gibt nur eine Bedingung:
- 1. Die Normalenvektoren dürfen nicht linear abhängig sein. Sie müssen also linear unabhängig sein.
Das ist das Gegenteil der ersten Bedingung bei identisch/parallel und die einzige, die erfüllt sein muss. (Ähnlich wie bei Geraden im zweidimensionalen Raum - diese schneiden sich auch automatisch, wenn sie nicht parallel und nicht identisch sind.)
6. Links
Wieder zwei kleine Videos zum Thema:
- Einmal, wie man die Lagebeziehungen zwischen einer Ebene in Koordinatenform und einer in Normalenform errechnet: Video ansehen
- Und das zweite zeigt die Rechnung mit zwei Ebenen in Parameterform.
Kommentare (7)
Von neu nach altWir bitten um ihr Verständnis.