1. Einleitung
Im Artikel zur Darstellung wurde bereits die allgemeine Formel einer vektoriellen Geraden beschrieben:
Bei dieser Formel steht
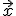
für einen Vektor, der auf jeden beliebigen Punkt auf der Geraden zeigt - je nachdem was man im rechten Teil der Gleichung für 
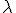
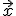
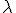
einsetzt. Will man nun herausfinden, ob ein Punkt auf einer bestimmten Geraden liegt, so bietet es sich an, diesen Punkt einfach für einzusetzen. Kann man dann ein finden, durch welches sich genau dieser Punkt ergibt, so liegt er auf der Geraden. Erhält man ein widersprüchliches Ergebnis, so liegt er nicht auf der Geraden.2. Formel
Allgemein:
In dieser allgemeinen Formel müssen alle drei
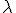
den gleichen Wert ergeben - dann liegt der Punkt auf der Geraden. Weicht auch nur ein Lambda ab, so kann der Punkt nicht von der Geraden dargestellt werden und liegt somit nicht auf dieser - oder man hat sich verrechnet.Beispiel:
In diesem Beispiel liegt der Punkt P also auf der Geraden. Er ergibt sich, wenn man für
2 einsetzt.
Kommentare (15)
Von neu nach altWir bitten um ihr Verständnis.
Hatte das problem beim programmieren, dass durch null geteilt wurde, wenn eine Komponente von r=0 war! Aber so ist es besser!
Ziel ist ja nicht einen Punkt auszurechnen sondern nur etwas festzustellen:
Die Vektoren (x-s) und (x-r) müssen linear abhängig sein (gleiche Richtung)
-> Kreuzprodukt von (x-s) und (x-r) muss der Nullvektor sein.
(x-s) X (x-r) = 0 einfach mit Sarrus ausrechen. Fertig.
keine sorge
die pfeile über den buchstaben geben doch an dass es sich um vektoren handelt!
außerdem stimmt dein gegenbeispiel nicht.
lg