1. Einleitung
Man kann Geraden auch mit Hilfe von Vektoren darstellen. Dazu zerlegt man die Geraden zunächst in zwei Teile:
- Ein beliebiger Punkt auf der Geraden. Dieser Punkt dient dazu, die Position der Geraden im Raum zu bestimmen. Von hier aus wird die weitere Ausrichtung festgelegt.
Der Vektor, der auf diesen Punkt zeigt, wird als "Stützvektor" bezeichnet. - Ein weiterer Vektor, der vom festgelegten Punkt aus die Richtung der Geraden beschreibt.
Dieser Vektor ist der sogenannte "Richtungsvektor".
Um nun jeden beliebigen Punkt auf der Geraden darstellen zu können, setzt man eine Variable (z.B. Lambda:
) vor den Richtungsvektor und kann dadurch dessen Länge verändern.Mit Stützvektor+100*Richtungsvektor zeigt man logischerweise auf einen anderen Punkt, als wenn man Stützvektor+(-2)*Richtungsvektor rechnet.
2. Darstellung
Allgemein:
ist ein Stützvektor
ist ein Richtungsvektor ist eine Variable, die die Länge des Richtungsvektors verändert.
Hier kann man erkennen, dass sich der Ortsvektor zu Punkt x (
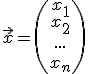) auf der Geraden ergibt, indem man auf einen Punkt auf der Geraden zeigt (Stützvektor ) und von dort aus eine bestimmte Strecke in eine bestimmte Richtung zurücklegt (Richtungsvektor ). Will man keinen Punkt auf der Geraden festlegen, sondern stattdessen die gesamte Gerade über eine Formel darstellen, so setzt man einfach keinen Wert für ein.Beispiel:
Beispiel:
Beispiel:
Beispiel:
Beispiel:
Die Gerade des letzten Beispiels ginge durch den Nullpunkt, da kein Stützvektor angegeben bzw. dieser
lautet.3. Links
Ein kleines Video dazu wie man eine Gerade in der Vektorrechnung bildet: Video
Kommentare (9)
Von neu nach altWir bitten um ihr Verständnis.
evtl. wäre es noch gut mit einzubauen, dass diese Variante (Gleichung) auch Parameterform genannt wird. (Zwecks Aufgabenstellung).
Arno, interessant.
Is doch schnurzwumpe was da steht.