1. Einleitung
Die Normalenform wird grundsätzlich anders gebildet als die Parameterform. Wie ihr Name schon andeutet, spielt der Normalenvektor der Ebene eine große Rolle.
Die Theorie für die Normalenform ist folgende: Zeigt man mit einem Ortsvektor auf einen Punkt im Raum, so kann man zu diesem Ortsvektor beliebig viele orthogonale Vektoren finden. Lässt man alle diese Vektoren an dem Punkt starten, auf den der Ortsvektor zeigt, dann liegen all diese Vektoren in einer Ebene - und bilden damit eine.
Um die Normalenform einer Ebene zu bilden braucht man also nur:
- Einen Normalenvektor
- Einen Punkt in der Ebene (auf den der Ortsvektor dann zeigt)
Das ist schon alles. Alle anderen Vektoren, die man braucht, um z.B. auf einen bestimmten Punkt in der Ebene zu zeigen, ergeben sich einfach dadurch, dass sie senkrecht (also orthogonal) zum Normalenvektor sind.
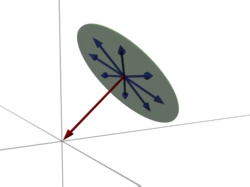 Bild 1: Eine Ebene in Normalenform. In rot der Richtungsvektor und der gegebene Punkt. Grün (leicht durchsichtig) die Ebene, blau (leicht durchsichtig) ein Teil der Vektoren, die in der Ebene liegen und im rechten Winkel zum Normalenvektor liegen.
Bild 1: Eine Ebene in Normalenform. In rot der Richtungsvektor und der gegebene Punkt. Grün (leicht durchsichtig) die Ebene, blau (leicht durchsichtig) ein Teil der Vektoren, die in der Ebene liegen und im rechten Winkel zum Normalenvektor liegen. 2. Darstellung
allgemeine Darstellungsform:
Wobei hier
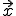
jeder beliebige Punkt in der Ebene ist.
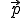
ist ein bereits definierter Punkt in der Ebene und
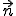
ist der Normalenvektor der Ebene.
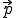
und
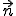
müssen also festgelegt werden, damit die Ebene definiert ist. (Siehe auch die Bedingungen oben:
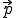
ist der Punkt in der Ebene,
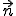
ist der Normalenvektor der Ebene.)
Es wird hierbei ein Vektor zwischen
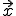
und
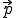
gebildet, der völlig variabel ist, da
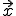
nicht bestimmt wird -
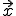
zeigt ja schließlich auf
jeden beliebigen Punkt auf der Ebene.
Dieser sich ergebende Vektor (aus
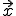
und
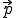
) geht vom Punkt p aus und wird mit dem Normalenvektor
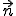
der Eben multipliziert. Das Skalarprodukt aus diesem Vektor und
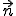
muss 0 ergeben - die beiden Vektoren müssen also orthogonal zueinander liegen (siehe auch
Orthogonalität).
Beispiel:
In diesem Beispiel ist der festgelegte Punkt in der Ebene
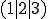
.
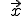
minus dem Ortsvektor zu diesem Punkt ergibt einen variablen Vektor (da x nicht klar definiert ist), der vom Punkt
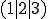
ausgeht. Dieser variable Vektor wird mit dem Normalenvektor der Ebene
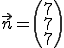
multipliziert. Das Skalarprodukt aus diesen beiden Vektoren muss 0 ergeben. Erst dadurch wird der Vektor genügend eingeschränkt, um vom Punkt
aus abzugehen
und in der Ebene zu liegen, also senkrecht zum Normalenvektor.

Kommentare (11)
Von neu nach altWir bitten um ihr Verständnis.
Der Vektor in rot müsste der Normalenvektor sein oder!??
Da der Ortsvektor (bzw. "Ortspunkt") aber meist der einzige Vektor (Punkt) ist, der dir gegeben ist, nimmt man ihn auch in der Regel.
Der rote Vektor soll die Orthogonale darstellen. Die orthogonale ist ja immer die Senkrechte zu einer anderen Geraden oder Ebene (in dem Beispiel die Ebene). Diese Orthogonale zeigt deswegen in die entgegengesetzte Richtung, weil sie ja senkrecht von der Ebene ausgeht.
So würde ich mir das jetzt erklären. Ich hoffe es hilft die weiter.