1. Einleitung
Wenn man mit Ebenen arbeitet, dann wird man sehr häufig herausfinden müssen, ob ein bestimmter Punkt in einer Ebene liegt. Das ist aber keine schwierige Aufgabe und in den meisten Fällen kann man die Antwort auf diese Frage schon in weniger als einer Minute gefunden haben. Es hängt aber auch davon ab, in welcher Form die Ebene gegeben ist:
- Koordinatenform: Rechnung geht am schnellsten
- Normalenform: Rechnung dauert geringfügig länger
- Parameterform: Rechnung benötigt deutlich mehr Zeit
Wenn möglich sollte man also immer die Koordinatenform wählen, sofern diese gegeben ist.
2. Allgemeines Vorgehen
In jeder Ebenenform gibt es einen Vektor, der auf jeden Punkt zeigt, der in der Ebene liegt. Üblicherweise:
Wenn dieser Vektor auf jeden Punkt zeigt, der in der Ebene liegt, was spricht dann dagegen, einfach mal für
- Man hat einen Punkt von dem man wissen will, ob er in der Ebene liegt.
- Man bildet den Ortsvektor zu diesem Punkt.
- Man ersetzt
mit diesem Ortsvektor.
- Dann wird überprüft, ob die Gleichung "aufgeht", also ob man ein wahres Ergebnis erhält. Ist das Ergebnis wahr, dann liegt der Punkt in der Ebene. Ansonsten liegt er nicht in ihr.
3. Beispiel: Parameterform
Wie auch weiter oben bereits gesagt, ist es bei der Parameterform noch am langwierigsten zu überprüfen, ob ein Punkt in der Ebene liegt.
Beispiel: Punkt liegt in Ebene
Gegeben:
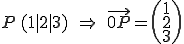
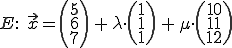
Ein lineares Gleichungssystem wird aufgestellt:
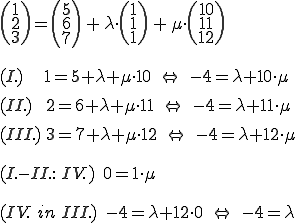
Setzt man also in die Ebenengleichung für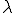 den Wert -4 und für
den Wert -4 und für 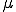 den Wert 0 ein, dann erhält man den Punkt P. Der Punkt liegt also in der Ebene.
den Wert 0 ein, dann erhält man den Punkt P. Der Punkt liegt also in der Ebene.
Ein lineares Gleichungssystem wird aufgestellt:
Setzt man also in die Ebenengleichung für
4. Beispiel: Normalenform
Schon deutlich besser geeignet für solch eine Rechnung ist die Normalenform. Auch hier setzt man einfach wieder für
Beispiel: Punkt liegt in Ebene
Gegeben:
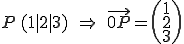
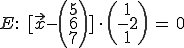
Man muss nun einfach den Ortsvektor zu P einsetzen und alles ausmultiplizieren:
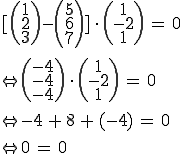
Die Aussage 0 = 0 ist wahr und daher liegt der Punkt in der Ebene.
Man muss nun einfach den Ortsvektor zu P einsetzen und alles ausmultiplizieren:
Die Aussage 0 = 0 ist wahr und daher liegt der Punkt in der Ebene.
Beispiel: Punkt liegt nicht in Ebene
Die gesamte Rechnung ist nahezu identisch mit dem Beispiel für Punkt liegt in Ebene. Es wurde nur die x3-Koordinate von 3 auf 300 gesetzt, sodass der Punkt nicht mehr in der Ebene liegt.
Gegeben:
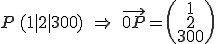
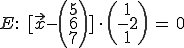
Man muss nun einfach den Ortsvektor zu P einsetzen und alles ausmultiplizieren:
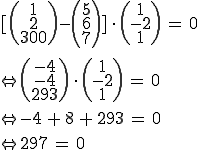
Das Ergebnis 297 = 0 ist offensichtlich nicht wahr und daher liegt der Punkt nicht in der Ebene.
Man muss nun einfach den Ortsvektor zu P einsetzen und alles ausmultiplizieren:
Das Ergebnis 297 = 0 ist offensichtlich nicht wahr und daher liegt der Punkt nicht in der Ebene.
5. Beispiel: Koordinatenform
Die Berechnung bei der Koordinatenform ist sehr vergleichbar zu der bei der Normalenform. Auch hier muss man prüfen, ob das Endergebnis ein wahres oder eine unwahres ist. Man kann sich aber die Berechnung des Skalarprodukts sparen, stattdessen besteht die ganze Rechnung nur aus ein bisschen Addition und Multiplikation. Daher ist es auch am einfachsten bei der Koordinatenform zu prüfen, ob ein Punkt in der Ebene liegt.
Beispiel: Punkt liegt in Ebene
Gegeben:
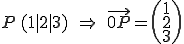
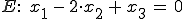
Ortsvektor zu P in E eingesetzt und danach ausmultipliziert:
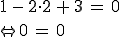
Das Ergebnis 0=0 ist wahr, daher liegt der Punkt in der Ebene.
Ortsvektor zu P in E eingesetzt und danach ausmultipliziert:
Das Ergebnis 0=0 ist wahr, daher liegt der Punkt in der Ebene.
Beispiel: Punkt liegt nicht in Ebene
Gegeben:
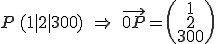
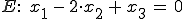
Ortsvektor zu P in E eingesetzt und danach ausmultipliziert:
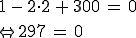
Das Ergebnis 297=0 ist offensichtlich nicht wahr, daher liegt der Punkt auch nicht in der Ebene.
Ortsvektor zu P in E eingesetzt und danach ausmultipliziert:
Das Ergebnis 297=0 ist offensichtlich nicht wahr, daher liegt der Punkt auch nicht in der Ebene.
Kommentare (28)
Von neu nach altWir bitten um ihr Verständnis.
unser lehrer ist erkankt und sie sind auch "so" (übers internet) viel besser als mein lehrer!!
ich werde auf diese seite zurückgreifen :) danke danke danke!!
unser lehrer ist erkankt und sie sind auch "so" (übers internet) viel besser als mein lehrer!!
ich werde auf diese seite zurückgreifen :) danke danke danke!!