1. Einleitung
Die Koordinatenform ist letztlich nichts anderes als die ausmultiplizierte Version der Normalenform einer Ebene. Daher ist sie auch auf die selbe Weise aufgebaut: In der Gleichung kommt der Normalenvektor der Ebene vor, sowie ein Punkt der in der Ebene liegt. Das reicht aus, um die Ebenengleichung zu bilden.
Die Koordinatenform hat den Vorteil, dass man mit ihr innerhalb kürzester Zeit ausrechnen kann, ob ein bestimmter Punkt in der Ebene liegt.
2. Darstellung
Allgemein:
Dabei sind n1, n2 und n3 die einzelnen Komponenten des Normalenvektors der Ebene:
Die Variable "d" gibt Hinweis auf den Abstand der Ebene vom Ursprung. Diesen Abstand erhält man, indem man "d" durch die Länge des Normalenvektors
Beispiel:
3. Koordinatenform aus Normalenform errechnen
Wie oben bereits beschrieben, muss man eine Ebenengleichung, die in Normalenform vorliegt, nur ausmultiplizieren, um die Koordinatenform zu erhalten.
Beispiel:
Normalenform:
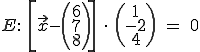
Die Koordinatenform erhält man durch ausmultiplizieren.
Verwendet wird das Skalarprodukt, beachtet werden sollte, dass dabei gilt
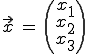
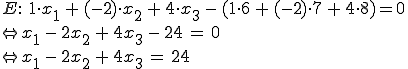
Die Koordinatenform erhält man durch ausmultiplizieren.
Verwendet wird das Skalarprodukt, beachtet werden sollte, dass dabei gilt
Kommentare (11)
Von neu nach altWir bitten um ihr Verständnis.
Das d alleine ist das Skalarprodukt zwischen dem Orts- und dem Normalenvektor.
Das Skalerprodukt ist auch definiert als <x,y>=|x| * |y| * cos w(x,y), d.h. das Skalarprodukt ist das Produkt aus den Vektorlängen und dem Kosinus des Winkels zwischen x und y.
Danke für den Hinweis.