1. Einleitung
In diesem Artikel wird gezeigt, wie man aus verschiedenen Vorgaben eine Gleichung für eine Ebene bildet. Es wird dabei häufig die Parameterform verwendet, da sie aus den meisten Vorgaben am einfachsten zu erstellen ist. Sollte durch die Aufgabe eine ganz spezielle Form vorgegeben sein, dann ist es gewöhnlich am einfachsten, die Ebene wie hier vorgeführt zu erstellen und danach diese Ebenengleichung in eine andere Form umzurechnen. Also: Erst alles wie hier, dann einfach umrechnen (sofern eine andere Form verlangt ist).
Grundsätzlich ist das Bilden von Ebenen sehr einfach. Man muss dabei eine Ebene aus verschiedenen Vorgaben kreieren, z.B. die, dass drei gegebene Punkte in der neuen Ebene liegen sollen. Das Vorgehen ist jedes mal ähnlich. Man verwendet in den meisten Fällen die Parameterform, da sie häufig am einfachsten zu bilden ist. Da für die Parameterform immer ein Stützvektor und zwei Richtungsvektoren benötigt werden, muss man sich fragen, wie man aus den Vorgaben einen Punkt und zwei Vektoren "herausfiltern" kann, die in der neuen Ebene liegen. Hat man z.B. drei Punkte als Vorgabe, dann nimmt man sich einfach einen der drei Punkte als Stützvektor und bildet zwei Vektoren zwischen den Punkten. Die beiden so gefundenen Vektoren verwendet man als Richtungsvektoren - und schon hat man eine Ebenengleichung.
Wiederholung: Parameterform
Die Parameterform wird folgendermaßen aufgeschrieben:
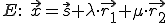
Dabei ist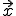 der Ortsvektor auf jeden beliebigen Punkt in der Ebene (je nachdem, welche Werte man für die Variablen einsetzt, erhält man andere Punkte, die aber alle in der Ebene liegen). Der Vektor
der Ortsvektor auf jeden beliebigen Punkt in der Ebene (je nachdem, welche Werte man für die Variablen einsetzt, erhält man andere Punkte, die aber alle in der Ebene liegen). Der Vektor 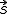 ist der Stützvektor der Ebene, also der Ortsvektor zu einem Punkt, der in der Ebene liegt. Die Vektoren
ist der Stützvektor der Ebene, also der Ortsvektor zu einem Punkt, der in der Ebene liegt. Die Vektoren 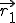 und
und 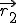 sind die Richtungsvektoren der Ebene.
sind die Richtungsvektoren der Ebene.
Dabei ist
2. Ebene bilden aus: 3 Punkten
Das grundsätzliche Vorgehen hierbei ist wie folgt:
- 1. Entscheidung/Aufgabe: Die neue Ebene soll in Parameterform gebildet werden.
- 2. Einen beliebigen Punkt wählen: Das wird der Stütvektor.
- 3. Zwei Vektoren zwischen zwei jeweils verschiedenen und beliebigen Punkten bilden. (Es dürfen nur nicht zweimal die selben Punkte sein!).
- 4. Die beiden neuen Vektoren auf lineare Abhängigkeit prüfen.*
- 5. Alles in eine Ebenengleichung packen.
*= Das ist recht wichtig, denn wenn die drei Punkte alle genau auf einer Geraden liegen würden, dann würde man zwei Vektoren mit unterschiedlicher Länge, aber gleicher (oder genau entgegengesetzter) Richtung erhalten. Das ist ein Problem, denn wenn man die beiden Vektoren verwenden würde, dann würde man keine Ebenengleichung erhalten, sondern eine Geradengleichung (die nur auf den ersten Blick wie eine Ebenengleichung aussehen würde). Für drei Punkte, die auf einer Geraden liegen, kann man keine eindeutige Ebenengleichung finden!
Beispiel:
Gegeben:
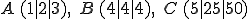
Aufgabe könnte lauten: Bilden Sie eine Ebene in der die drei Punkte A, B und C liegen.
1. Schritt: Wir wollen die Ebene in Parameterform schreiben.
2. Schritt: Ein beliebiger Punkt der Ebene wird als Stützvektor verwendet (hier A):
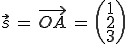
3. Schritt: Zwei Richtungsvektoren werden gebildet (hier aus den Vektoren AB und AC):
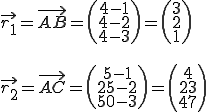
4. Schritt: Auf lineare Abhängigkeit prüfen:
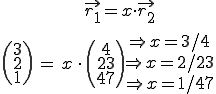
Es lässt sich kein einheitliches x finden, daher sind die beiden Vektoren linear unabhängig.
5. Schritt: Alles in eine Ebenengleichung:
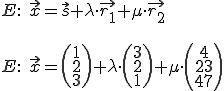
Aufgabe könnte lauten: Bilden Sie eine Ebene in der die drei Punkte A, B und C liegen.
1. Schritt: Wir wollen die Ebene in Parameterform schreiben.
2. Schritt: Ein beliebiger Punkt der Ebene wird als Stützvektor verwendet (hier A):
3. Schritt: Zwei Richtungsvektoren werden gebildet (hier aus den Vektoren AB und AC):
4. Schritt: Auf lineare Abhängigkeit prüfen:
Es lässt sich kein einheitliches x finden, daher sind die beiden Vektoren linear unabhängig.
5. Schritt: Alles in eine Ebenengleichung:
3. Ebene bilden aus: 2 Geraden
Das Prinzip ist hierbei, dass man sich die beiden Richtungsvektoren der Geraden nimmt und dazu einen der beiden Stützvektoren. Damit hat man für die Ebene zwei Richtungsvektoren und einen Punkt in der Ebene, also alles was man braucht.
Bevor man das ganze macht muss man sich aber eines ins Bewusstsein rufen: Das oben genannte Vorgehen funktioniert nur bei Geraden, die sich schneiden. Ist also durch die Aufgabe vorgegeben, dass sie sich schneiden, dann ist es recht einfach. Ansonsten hängt alles davon ab, wie die Geraden zueinander liegen. Folgende Fälle gibt es:
- Geraden schneiden: Wie oben schon gesagt ist die Ebene leicht zu bilden. Einfach einen Stützvektor und die Richtungsvektoren der beiden Geraden nehmen.
- Geraden parallel: Würde man hier einfach die beiden Richtungsvektoren verwenden, dann würde man am Ende keine Ebenengleichung, sondern eine Geradengleichung erhalten (die aussähe wie eine Ebenengleichung). Das liegt daran, dass beide Richtungsvektoren linear abhängig wären, also grob gesagt auf einer Linie liegen würden. Man muss hier einen Vektor bilden, der "zwischen" beiden Geraden liegt und diesen als einen der beiden Richtungsvektoren verwenden. Ansonsten funktioniert alles genauso wie bei schneidenden Geraden.
- Geraden identisch (liegen "ineinander"): Auch hier würde man eine Geradengleichung erhalten, würde man beide Richtungsvektoren verwenden. Wenn verlangt wird, aus zwei Geraden eine Ebene zu bilden, heißt es aber gewöhnlich nur, dass beide Geraden in der Ebene liegen sollen. Daher kann man für zwei identische Geraden unendlich viele verschiedene Ebenengleichungen aufstellen, die alle die beiden Geraden einschließen. Man kann also einen der beiden Richtungsvektoren beliebig wählen - er darf nur nicht linear abhängig vom zweiten Richtungsvektor sein. Der zweite Richtungsvektor ist der Richtungsvektor einer der beiden Geraden.
- Geraden liegen windschief: Einer der einfachen Fälle. Hier gibt es schlichtweg keine Ebenengleichung, die beide Ebenen einschließt.
Damit's etwas übersichtlicher wird gibt es jetzt das ganze Vorgehen nochmal in einigen einfachen Schritten:
- 1. Entscheidung/Aufgabe: Die neue Ebene soll in Parameterform gebildet werden.
- 2. Prüfen: Wie liegen die Geraden zueinander?
- 3.1. Windschief: Glück gehabt, hier gibt's keine Ebenengleichung. Man kann aufhören mit der Aufgabe.
- 3.2. Identisch: 1 Richtungsvektor einer Geraden, 1 beliebiger Richtungsvektor der nicht linear abhängig vom ersten Richtungsvektor ist, 1 Stützvektor von einer der beiden Geraden.
- 3.3. Parallel: 1 Richtungsvektor einer Geraden, 1 Richtungsvektor zwischen den Geraden bilden (am besten hierfür die beiden Stützvektoren verwenden), 1 Stützvektor einer der beiden Geraden.
- 3.4. Schneiden: 1 Richtungsvektor einer Geraden, 1 Richtungsvektor der anderen Geraden, 1 Stützvektor einer der beiden Geraden.
- 4. Die beiden gewählten Richtungsvektoren und den Stützvektor in eine Ebenengleichung packen.
Wichtig ist also bei dieser Aufgabe sich klar zu machen, dass 90 Prozent der Arbeit nur daraus besteht zu erkennen, wie die Geraden zueinander liegen.
4. Ebene bilden aus: 1 Punkt, 1 Gerade
Hier muss man sich zum Glück nicht so viel Arbeit machen wie bei den zwei Geraden (siehe oben). Man muss nur überprüfen, ob der Punkt auf der Geraden liegt. Liegt er nicht auf der Geraden, dann kann man eine eindeutige Ebene bilden, indem man den Richtungsvektor der Geraden nimmt, einen Vektor zwischen Punkt und Gerade zieht und den Punkt als Stützvektor der neuen Ebene verwendet. Liegt der Punkt auf der Geraden, dann lässt sich keine eindeutige Ebene bestimmen. In diesem Fall gibt es unendlich viele verschiedene Ebenen, die sowohl Punkt als auch Gerade einschließen.
- 1. Entscheidung/Aufgabe: Die neue Ebene soll in Parameterform gebildet werden.
- 2. Prüfen: Liegt der Punkt auf der Geraden?
- 3.1. Wenn ja: Es lässt sich keine eindeutige Ebene bestimmen. Man verwendet den Richtungsvektor der Geraden und wählt einen zweiten beliebig (aber nicht linear abhängig vom ersten). Als Stützvektor kann der Punkt herhalten.
- 3.2. Wenn nein: Liegt der Punkt nicht auf der Geraden, dann lässt sich eine eindeutige Ebene bestimmen. Man wählt den Richtungsvektor der Geraden als einen Richtungsvektor, einen Vektor zwischen Punkt und Gerade als zweiten Richtungsvektor, den Stützvektor der Geraden als Stützvektor der Ebene.
- 4. Alles in eine Parameterform packen.
Kommentare (28)
Von neu nach altWir bitten um ihr Verständnis.
Hier müsste >Ebenen< durch >Geraden< ersetzt werden.
Please take care of the copyrights!
Thanks !