1. Einleitung
Die Berechnung des Abstandes zwischen einem Punkt und einer Geraden ist eine der schwereren Übungen in der Abstandsberechnung, aber nicht unschaffbar.
Grundsätzlich gilt wieder, dass mit "Abstand" der kürzeste Abstand zwischen Punkt und Gerade gemeint ist. Würde man diesen Abstand als Gerade abbilden, dann würde die Gerade im rechten Winkel (also orthogonal) zur gegebenen Geraden liegen.
Das grobe Vorgehen ist, dass man aus dem gegebenen Punkt und dem Richtungsvektor der Geraden eine Hilfsebene baut. Diese Hilsebene liegt dann orthogonal zur Geraden und enthält den gegebenen Punkt. Nun wird bestimmt, wo sich Gerade und Hilfsebene schneiden. Zwischen diesem Schnittpunkt und dem gegeben Punkt wird der Vektor bestimmt. Die Länge dieses Vektors ist der Abstand zwischen Punkt und Gerade.
Nochmal etwas genauer:
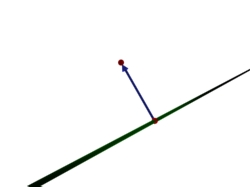
- Schritt 1: Punkt und Gerade sind gegeben. (Punkt ist hier rot, Gerade grün)
- Schritt 2: Richtungsvektor wird der Geraden entnommen. (Hier schonmal an den gegebenen Punkt angehängt. Liegt übrigens an der Kameraperspektive, dass das so aussieht als ob der in eine andere Richtung zeigen würde als die Gerade.)
- Schritt 3: Aus dem gegebenen Punkt und dem Richtungsvektor der Geraden wird eine Hilfsebene zusammengesetzt. (Hier bräunlich, leicht durchsichtig)
- Schritt 4: Schnittpunkt zwischen Hilfsebene und Gerade wird ermittelt. (Der andere kleine rote Punkt auf der Geraden)
- Schritt 5: Vektor zwischen Schnittpunkt und gegebenen Punkt wird gebildet. (Vektor in blau, Hilfsebene ist jetzt ausgeblendet, da die eh nicht mehr gebraucht wird.)
- Schritt 6: Die Länge dieses Vektors wird bestimmt. Die Länge entspricht dem Abstand zwischen Gerade und Punkt.
2. Formel
Die allgemeine Form des Vorgehens wird hier mal nicht beschrieben, da das eh zu kompliziert werden würde.
Beispiel:
Schritt 1:
Gegeben:
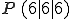
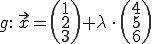
Schritt 2:
Der Richtungsvektor der Geraden lautet also:
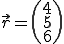
Schritt 3:
Aus Punkt P und r kann nun eine Ebene gebildet werden.
Dazu wird r als der Normalenvektor verwendet und die Ebene in Normalenform geschrieben.
Direkt dadrunter steht die Ebene in Koordinatenform (einfach ausmultipliziert mit Skalarprodukt).
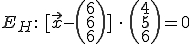
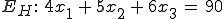
Schritt 4:
Jetzt wirds etwas schwieriger, denn der Schnittpunkt zwischen der Geraden und der Hilfsebene muss berechnet werden. Dazu setzt man die Geradengleichung bei der Hilfsebene ein:
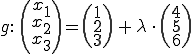
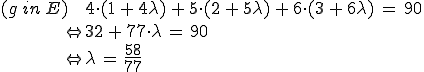
Jetzt weiß man wie der Wert für lambda sein muss, damit man den Schnittpunkt erhält. Diesen Wert muss man nun in die Geradengleichung einsetzen:
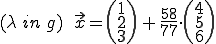
Wenn man das jetzt ausrechnet erhält man den recht krummen Schnittpunkt (S). (Alle Werte von diesem Punkt sind gerundet, daher sind auch alle weiteren Ergebnisse ab jetzt nur noch gerundet richtig.)
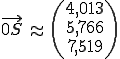
Schritt 5 und 6:
Nun bildet man den Vektor zwischen dem Schnittpunkt und dem gegebenen Punkt.
Die Länge dieses Vektors ist der Abstand zwischen Punkt und Gerade.
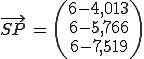
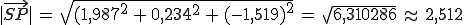
Der Abstand zwischen Punkt und Gerade beträgt also ungefähr 2,512 Längeneinheiten.
Gegeben:
Schritt 2:
Der Richtungsvektor der Geraden lautet also:
Schritt 3:
Aus Punkt P und r kann nun eine Ebene gebildet werden.
Dazu wird r als der Normalenvektor verwendet und die Ebene in Normalenform geschrieben.
Direkt dadrunter steht die Ebene in Koordinatenform (einfach ausmultipliziert mit Skalarprodukt).
Schritt 4:
Jetzt wirds etwas schwieriger, denn der Schnittpunkt zwischen der Geraden und der Hilfsebene muss berechnet werden. Dazu setzt man die Geradengleichung bei der Hilfsebene ein:
Jetzt weiß man wie der Wert für lambda sein muss, damit man den Schnittpunkt erhält. Diesen Wert muss man nun in die Geradengleichung einsetzen:
Wenn man das jetzt ausrechnet erhält man den recht krummen Schnittpunkt (S). (Alle Werte von diesem Punkt sind gerundet, daher sind auch alle weiteren Ergebnisse ab jetzt nur noch gerundet richtig.)
Schritt 5 und 6:
Nun bildet man den Vektor zwischen dem Schnittpunkt und dem gegebenen Punkt.
Die Länge dieses Vektors ist der Abstand zwischen Punkt und Gerade.
Der Abstand zwischen Punkt und Gerade beträgt also ungefähr 2,512 Längeneinheiten.
3. Anmerkungen
- Es kann empfehlenswert sein, vorher nachzuschauen, ob der gegebene Punkt auf der Geraden liegt. Denn dann ist der Abstand logischerweise 0 und man spart sich die lange Rechnerei.
4. Links
Noch zwei Videos passend zum Thema:
- Abstandsaufgabe 1: Eine Gerade und ein Punkt C auf der Geraden ist angegeben, nun soll errechnet werden, welche Punkte auf der Geraden einen bestimmten Abstand von C haben. Wird etwas anders gerechnet als das was hier angegeben wurde. Ist aber grundsätzlich nicht schwer.
- Abstandsaufgabe 2, ist ähnlich zu dem was hier steht.




Kommentare (141)
Von neu nach altWir bitten um ihr Verständnis.
d= |a x (p - r)| : |a|
(a) ist Richtungsvektor.
(p) ist der Vektor vom Ursprung zum Punkt
(r) ist ein Vektor vom Ursprung zu einem Punkt auf der Geraden
Bsp.: Punkt-Richtungsform einer Geraden:
x = r + (Lambda)*a
es heißt ja E: 4x1 + 5x2 + 6x3 = (jetzt wird die Ebene mit dem Punkz P mutlipliziert) 4x6+5x6+6x6 = 90
4x1 + 5x2 + 6x3 =90