1. Einleitung
Den Abstand eines Punktes von einer Ebene zu errechnen geht schnell.
Alles was man dafür machen muss ist nur, die Hessesche Normalenform der Ebene zu bilden und dann den Punkt darein einzusetzen.
2. Formel
Allgemein:
Gegeben ist ein Punkt und eine Ebene (in Koordinatenform).
Aus der Ebenengleichung kann man den Normalenvektor n entnehmen.
Da die Länge vom Normalenvektor ohnehin für die Hessesche Normalenform benötigt wird, wird sie gleich mitausgerechnet.
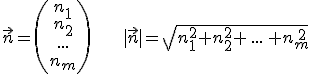
In diese Gleichung muss man nun den Ortsvektor zum Punkt P einsetzen (für die x1, x2 usw.).
Das Ergebnis ist der Abstand des Punktes P von der Ebene.
Beispiel:
Gegeben ist ein Punkt und eine Ebene in Koordinatenform.
Aus der Ebene kann man den Normalenvektor entnehmen und es wird direkt die Länge von dem errechnet.
Aus dem ganzen Kram bildet man nun die Hessesche Normalenform der Ebene (HNF):
Ortsvektor zu P in die HNF eingesetzt, ausgerechnet, fertig.
Der Abstand zwischen Ebene und Punkt beträgt ungefähr 367,554 Längeneinheiten.
3. Anmerkungen
- Wenn der Abstand zwischen Ebene und Punkt 0 ist, dann liegt der Punkt logischerweise in der Ebene.
- Wenn die Ebene nicht in Koordinatenform gegeben ist, dann muss man die Gleichung der Ebene in diese Form umrechnen.
Kommentare (58)
Von neu nach altWir bitten um ihr Verständnis.
Großes Lob an den Autor.