Abstand Gerade von Gerade (Thema: Vektorrechnung)

1. Einleitung

Der Abstand zweier Geraden voneinander wird definiert durch den kürzesten Abstand zwischen beiden. Man sucht also die beiden Punkte auf einer Geraden, die so nah wie möglich zueinander liegen. Sozusagen wie die Luftlinie zwischen zwei Städten.
Es gibt aber leider keine Formel, die man immer anwenden kann, um den Abstand zweier Geraden zu ermitteln. Stattdessen gibt es insgesamt drei verschiedene Vorgehensweisen. Wie man rechnen muss, bestimmt sich durch die Lage der beiden Geraden zueinander:

• Die Geraden schneiden sich:
  Hier kann man sich ordentlich freuen, denn die beiden am nächsten zueinander liegenden Punkte auf den beiden Geraden liegen logischerweise genau im Schnittpunkt. Damit ist der Abstand entsprechend 0.
• Die Geraden liegen parallel zueinander:
  Hier gibt es nicht zwei eindeutig bestimmbare Punkte, die am nächsten zueinander liegen, sondern unendlich viele. Das macht die ganze Sache glücklicherweise aber nicht viel schwerer, denn es gibt immer einen kürzesten Abstand, auch wenn der hier an mehreren Stellen gilt. Um den bei parallelen Geraden zu bestimmen sucht man sich einfach einen Punkt, der auf einer der Geraden liegt und bestimmt den Abstand dieses Punktes von der anderen Geraden.
• Die Geraden liegen windschief zueinander:
  Das ist der wohl schwerste Fall. Grob gesagt bildet man aus den Richtungsvektoren beider Geraden eine Ebene, die in einer der beiden Geraden liegt. Dann errechnet man den Abstand der anderen Geraden zu dieser Ebene. Das Ergebnis ist der kürzeste Abstand zwischen beiden Geraden.

2. Geraden schneiden sich

Wie schon oben gesagt, bedarf das keiner speziellen Rechnung und der Abstand ist immer Null. Um herauszufinden ob sich beide Geraden schneiden setzt man sie einfach wie üblich gleich.

3. Geraden liegen parallel

Liegen zwei Geraden parallel zueinander, so kann man den Abstand ausrechnen, indem man sich auf der einen Geraden einen Punkt nimmt und den Abstand von diesem Punkt zur anderen Geraden ausrechnet. Traditionell bietet es sich dafür an, den Stützvektor einer der beiden Geraden zu nehmen. Der Rest ist Abstandsberechnung zwischen Punkt und Gerade.

4. Geraden liegen windschief zueinander

Der schwierigste Fall in der Abstandsberechnung zwischen zwei Geraden. Um den Abstand hier zu erhalte, bildet man zunächst eine Hilfsebene. Als Richtungsvektoren der Hilfsebene verwendet man die Richtungsvektoren der beiden Geraden. Als Stützvektor nimmt man den Stützvektor einer der beiden Geraden. Dadurch erhält man eine Ebene, in der eine der beide Geraden liegt (die, deren Stützvektor verwendet wurde). Die andere Gerade schneidet die Ebene aber nicht, sondern läuft parallel zu dieser (ihr Richtungsvektor kommt ja auch in der Ebene vor). Den Abstand der beiden Geraden kann man dann berechnen, indem man den Abstand der Ebene zu der Geraden, die nicht in der Ebene liegt, bestimmt. Also in Kurzform:

• Zwei windschiefe Geraden gegeben (z.B. g und h)
• Hilfsebene bilden: Als Richtungsvektoren die Richtungsvektoren der Geraden. Als Stützvektor der Stützvektor einer Geraden (z.B. g).
• Eine Gerade liegt dann in der Hilfsebene (hier: g), eine liegt parallel zu dieser (hier: h).
• Abstand der parallelen Geraden zur Ebene bestimmen (also hier: Abstand h zu Hilfsebene)

Beispiel:

Aus Gerade g und Gerade h wird die Hilfsebene gebildet.
Dazu verwendet man den Stützvektor von g und die Richtungsvektoren von g und h:



Um den Abstand eines Punktes, der auf Gerade h liegt, von diese Ebene zu bestimmen brauchen wir die Hessesche Normalenform (HNF) der Ebene. Um die zu erhalten müssen wir aber erst die Koordinatenform errechnen, für die wir wiederum einen Normalenvektor der Ebene brauchen. Der Normalenvektor wird mit Hilfe des Vektorprodukts aus den beiden Richtungsvektoren gebildet:



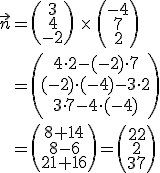
Die Länge des Normalenvektors brauchen wir später für die HNF:



Nun wird die Normalenform der Ebene gebildet, die wir dann einfach zur Koordinatenform umrechnen können:



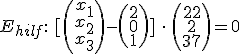
Das ganze ausmultiplizieren (mit Skalarprodukt) und man erhält die Koordinatenform:



Koordinatenform geteilt durch den Betrag vom Normalenvektor ergibt die HNF:



In die HNF muss man nun nur noch einen Punkt, der auf der Gerade h liegt, einsetzen. Dafür bietet sich deren Stützvektor an, denn der muss zwangsweise auf der Geraden liegen:



Ausgerechnet erhält man einen Abstand von ungefähr 1,71 Längeneinheiten. Das ist der Abstand von den beiden Punkten auf den Geraden, die zueinander am nächsten liegen.