1. Einleitung
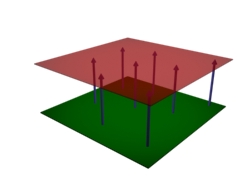
Als Abstand zwischen zwei Ebenen wird der kürzeste Abstand zwischen diesen bezeichnet. Würde man diesen Abstand als Gerade einzeichnen, dann würde diese Gerade immer rechtwinklig zu beiden Ebenen liegen. Eine vergleichbare Gerade, die nicht rechtwinklig zu beiden Ebenen liegt kann nie der kürzeste Abstand zwischen diesen sein. (Um aber Missverständnisse zu vermeiden: Es gibt nicht die eine Gerade, die den Abstand zwischen zwei Ebenen zeigt. Man könnte die Gerade nämlich beliebig verschieben. Nur die Länge der Geraden ist entscheidend. Siehe auch Bild 3 für ein besseres Verständnis).
Bild 1: Alle drei Geraden sind gleich lang. Aber nur die mittlere Gerade reicht bis zur oberen Ebene.
Bevor man den Abstand zweier Ebenen voneinander ausrechnet bietet es sich an zuerst zu schauen, ob die beiden Ebenen überhaupt parallel zueinander liegen. Nur wenn die Ebenen parallel sind, dann existiert überhaupt ein Abstand größer als Null. Sollten sie nicht parallel sein, dann schneiden sie sich an irgendeiner Stelle und haben somit zwangsweise an dieser Stelle den Abstand Null.
Bild 2: Zwei Ebenen schneiden sich, da sie nicht parallel und nicht identisch sind.
Man kann überprüfen, ob sich die Ebenen schneiden, indem man schaut ob die Normalenvektoren der beiden Ebenen voneinander linear abhängig sind. Sind sie das nicht, dann schneiden sich die Ebenen. Sind sie es, dann liegen sie mindestens parallel zueinander (sie können noch identisch sein). Um zu überprüfen, ob sie nun nur parallel sind, kann man einen Punkt einer Ebene bei der anderen einsetzen. Liegt dieser eingesetzte Punkt in der anderen Ebene, dann liegen auch alle anderen in dieser Ebene und die beiden Ebenen sind identisch (dann haben sie auch den Abstand 0).
Wenn die Ebenen parallel liegen, dann reicht es, von einer Ebene einen Punkt zu wählen und den Abstand dieses Punktes von der anderen Ebene zu bestimmen. Da die Ebenen parallel liegen, kann man logischerweise jeden beliebiegen Punkt von einer der beiden Ebenen nehmen. Der minimale Abstand dieses Punktes von der anderen Ebene ist immer der gleiche.
Bild 3: Zwei parallele Ebenen. Der Abstand ist an allen Stellen der gleiche.
2. Formel
Allgemein:
(Die allgemeine Vorgehensweise wird hier nicht mit Formeln unterlegt, da das eh unverständlich kompliziert werden würde)
- Gegeben: zwei Ebenen E1 und E2
- Normalenvektoren beider Ebenen finden.
- Prüfen, ob die Normalenvektoren linear abhängig sind.
Beantwortet die Frage ob sich die Ebenen schneiden. - Prüfen, ob ein Punkt der einen Ebene in der anderen liegt.
Beantwortet die Frage ob die Ebenen identisch sind. - Hessesche Normalenform (HNF) von einer der beiden Ebenen aufstellen. Z.B. von Ebene 1.
- Einen Punkt suchen, der in der anderen Ebene liegt (hier: Ebene 2).
- Punkt in die HNF einsetzen und so den Abstand bestimmen.
Man kann manchmal auch auf anderen Wegen herausfinden, ob die Ebenen parallel liegen. Im unteren Beispiel etwa wurde das einfacher gelöst. Der hier beschriebene Weg ist nur der Allgemeinste.
Beispiel:
Wie leicht erkennbar ist, sind die Normalenvektoren beider Ebenen gleich und damit linear abhängig. Nur die Abstände der Ebenen vom Nullpunkt aus sind unterschiedlich (1 und 10). Daher müssen die Ebenen parallel liegen.
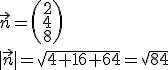
In die Hessesche Normalenform (HNF) wird ein Punkt eingesetzt, der auf der Ebene 2 liegt (hier: (5|0|0), einfach einsetzen und es kommt 10=10 heraus, also eine wahre Aussage).
Der Abstand der beiden Ebenen beträgt also etwa 0,982 Längeneinheiten.
Kommentare (44)
Von neu nach altWir bitten um ihr Verständnis.
das ist eine Formel ohne Namen zur Abstandsberechnung!
Man schaut einfach, für welche Werte von x1, x2 und x3 man eine wahre Aussage erhält:
Für x1 = 5 x2 =0 und x3 = 0 ist dies der Fall, denn man erhält:
E2: 2*5 + 4*0 + 8*0 = 10 ---> 10 = 10
Du könntest für x1, x2 und X3 auch andere Werte einsetzen, die zu einer wahren Aussage führen, beispielsweise E2: 2*0 + 4* 0,5 + 8*1 =10 ---> 10 = 10
Dann würde dein Punkt die Werte x1 = 0 ,x2 = 0,5 und X3 = 1 annehmen
hammer Seite, hat mir in den letzten Tagen sehr geholfen. Habe aber noch eine Frage, wie kommst du auf den Punkt P(5/0/0) bzw. einen beliebigen Punkt Element E2?
Danke dir!
danke!!