1. Einleitung
Ein Wendepunkt ist ein Punkt im Graphen, an dem dieser von einer Linksdrehung zu einer Rechtsdrehung wechselt, oder umgekehrt.
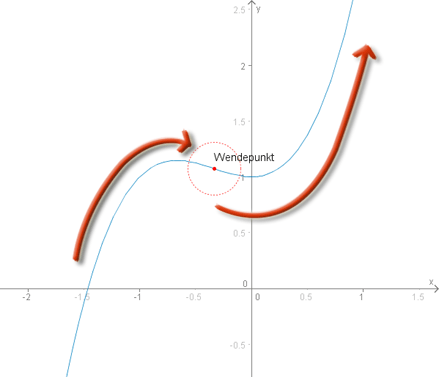
Angenommen der oben im Bild gezeigte Graph wäre eine Straße und man würde links unten auf dieser Straße ein Auto platzieren, welches in Richtung Wendepunkt fährt (und darüber hinaus), dann müsste der Fahrer zuerst das Lenkrad nach rechts drehen (=>Rechtskurve). Erst am Wendepunkt sollte er beginnen, das Lenkrad nach links zu drehen, um die vor ihm liegende Linkskurve zu "meistern".
2. Finden von Wendepunkten
Um Wendepunkte in einem Graphen zu finden benötigt man die 2. und 3. Ableitung. Bei allen x-Werten, bei denen die 2. Ableitung (also f''(x)) gleich Null ist, da könnte ein Wendepunkt liegen. Um zu überprüfen, ob da auch tatsächlich einer ist, muss man den entsprechenden x-Wert in die 3. Ableitung einsetzen und diese muss ungleich Null sein. Also in der Übersicht:
- f '' (x) = 0
- f ''' (x)
0
Beispiel:
2. Ableitung (f''(x)) wird gleich Null gesetzt:
Prüfung über 3. Ableitung:
Bei x=-1/3 liegt also ein Wendepunkt.
Nun muss dieser x-Wert noch in f(x) eingesetzt werden,
um den zugehörigen y-Wert zu erhalten.
Der Wendepunkt liegt also ungefähr bei (-1/3 | 1,074).
Vergleicht man das mit dem Wendepunkt oben im abgebildeten Graphen kommt dies auch hin
(der abgebildete Graph zeigt die im Beispiel verwendete Funktion).
Kommentare (18)
Von neu nach altWir bitten um ihr Verständnis.
Die Funktion f mit f(x)=x^5 hat eine Wendestelle bei x=0.
Die beiden im Text gebrauchten Ableitungen sind ja f''(x)=20x^3 und f'''(x)=60x^2.
Damit ist aber f'''(0) =0. D.h. an einer Wendestelle muss die dritte Ableitung nicht zwingend gleich Null sein.
Sehr kurz formuliert: WENN f''(x)=0 und f'''(x)<>0, DANN hat hat f an der Stelle x eine Extremstelle.
Im Text steht die Umkehrung, und die ist falsch, wie man am o.g. Bsp sieht.
Ihr braucht langsam wirklich Mods für Kommentare. Einige Kinder scheinen ja nichts besseres zu tun zu haben als ihr geistigen Ergüsse unter einer mathematischen Erläuterung zu posten.
hoffe das klappt morgen in der Mathe arbeit (:
hoffe das klappt morgen in der Mathe arbeit (:
für einen sattelpunkt ist doch die 1. bedingung f''(x)=0, f'''(x) ungleich 0 und f'(x)=0. also ein wendepunkt mit der steigung 0.
was ist wenn f´´´´= 0 ist und nicht ungleich 0 ?
was für ein punkt ist das dann?
Genau das hab ich gebraucht :P der Schlüssel hat mir gefehlt. Jetzt fällt mir alles easy :P. Aber Super gemahct dese Besfchreibung =)