Tangente an Punkt im Graphen (Thema: Analysis)

1. Einleitung

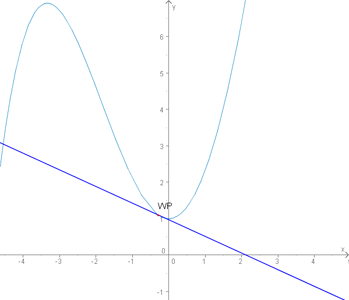
Während man in der Schule das Thema Differentialrechnung durchnimmt, wird man immer wieder Tangenten an Punkte im Graphen legen müssen. Besonders häufig muss man sie an Wendepunkten anlegen (dann genannt: Wendetangente).

Solch eine Tangente zu finden ist nicht sonderlich schwer. Man braucht lediglich den Punkt an dem sie anliegt (z.B. der Wendepunkt) und die Steigung, die man über die erste Ableitung herausfinden kann.

2. Tangente bilden

Man braucht folgende Komponenten, um die Tangente zu bilden:

• Den Punkt an dem sie anliegen soll mit x- und y-Koordinaten.
  Den muss man ggf. erst suchen, z.B. wenn man die Wendetangente bilden muss.
• Die Steigung an diesem Punkt.
  Diese findet man, indem man die x-Koordinate des Punktes an dem die Tangente anliegen soll in die erste Ableitung einsetzt.
• Die Punktsteigungsform einer Geraden.
  In die wird dann alles eingesetzt.

Man geht also folgendermaßen vor:

• Sofern die Koordinaten des Punktes nicht gegeben sind sucht man zuerst die x-Koordinate. Diese setzt man in f(x) ein, um die y-Koordinate des Punktes zu bestimmen.
• Man setzt die x-Koordinate in die erste Ableitung f ' (x) ein. Das Ergebnis ist die Steigung der Tangente.
• Man setzt x- und y-Koordinate sowie die Steigung in die Punktsteigungsform ein.
  Die Punktsteigungsform einer Geraden ist gegeben durch:
  
  wobei m die Steigung, px die x-Koordinate des Punktes und py die y-Koordinate des Punktes ist.