1. Einleitung
Als weiteres Instrument, um den Verlauf von Graphen zu beschreiben, nutzt man die Untersuchung auf "Symmetrie".
Man unterscheidet dabei zwischen zwei Arten von Symmetrie:
- Achsensymmetrie
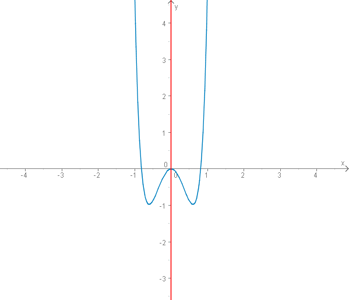
Ist ein Graph achsensymmetrisch, dann kann man den Teil rechts oder links von der y-Achse an der y-Achse spiegeln und erhält wieder den gleichen Graphen. Die beiden Teile des Graphen links und rechts von der y-Achse verlaufen also genau gleich.
- Punktsymmetrie
Der Graph kann an einem einzelnen Punkt gespiegelt werden und man erhält wieder den gleichen Graphen. In den meisten Fällen wird am Ursprung (0|0) gespiegelt.
2. Achsensymmetrie/Punktsymmetrie nachweisen
Die einfachste Möglichkeit, Achsen- oder Punktsymmetrie nachzuweisen, ist auf die Exponenten von x zu schauen. Sind alle gerade, dann liegt Achsensymmetrie vor. Sind alle ungerade, dann liegt Punktsymmetrie vor.
Beispielsweise wäre die Funktion
achsensymmetrisch, da alle Exponenten gerade sind.
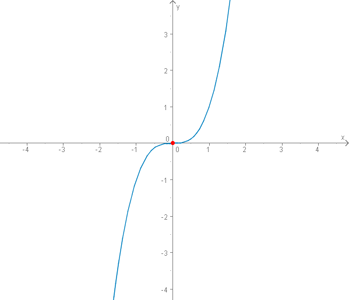
Hingegen wäre die Funktion
punktsymmetrisch, da alle Exponenten ungerade sind.
edit: Die obere Gleichung lautete zuvor
Wie in den Kommentaren richtig angemerkt wurde wäre das nicht punktsymmetrisch (zum Ursprung!), da gilt
3. mathematisches Vorgehen
Vor allem später wenn man etwas vertrauter mit der Differentialrechnung ist, wird man eher dazu tendieren, das mathematische Vorgehen vorzuziehen. Für dieses gelten die nachfolgenden Regeln:
Ist
(Sinngemäß: Es ist egal, ob man den x-Wert rechts oder links vom Ursprung aus einsetzt - man erhält immer den selben y-Wert.)
Ist
Kommentare (14)
Von neu nach altWir bitten um ihr Verständnis.
x^3 + 17-x^5 ist nicht das Gleiche wie x^3 - 17-x^5
x^3+17-x^5 = x^3-17-x^5 (falsche Aussage)
punktsymmetrisch, da alle Exponenten ungerade sind."
aber ist es nicht so, dass hinter der 17 ein gedachtes x^0 ist? das wäre ja dann gerade und somit dürfte die funktion ja weder punkt noch achsensymmetrisch sein.
-f(-x) = -(2(-x)*(-x)^3) = (2(x)*(x)^3) = f(x)
Methodisch ist es bei einer unbekannten Funktion jedoch sinnvoller immer mit f(-x) = ... zu rechnen, weil man dann sofort auf der anderen Seite sieht, ob entweder -f(x) bzw f(x) oder was ganz anderes rauskommt.
-f(-x) wäre dann ein Arbeitsschritt mehr, aber nicht falsch.
sollte das nicht: -f(x) = f(-x) sein