1. Einleitung
Der Sattelpunkt ist eine Sonderform des Wendepunktes. Er zeichnet sich dadurch aus, dass der Graph beim Sattelpunkt augenscheinlich parallel zur x-Achse verläuft. Es bildet sich also sozusagen eine Treppenstufe.
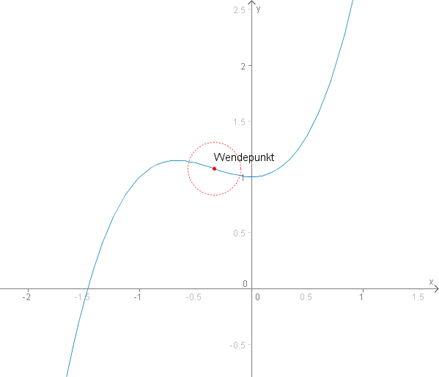
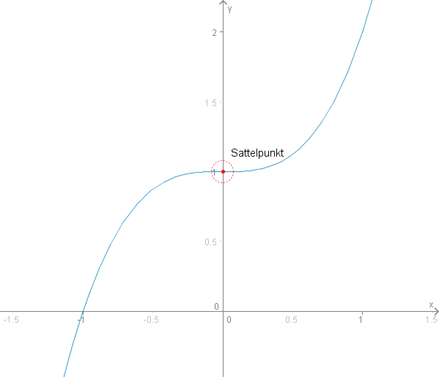
Hier mal ein bildlicher Vergleich zwischen Wendepunkt (zuerst) und Sattelpunkt (danach):
2. Sattelpunkt finden
Der Sattelpunkt errechnet sich nahezu genauso wie ein normaler Wendepunkt. Daher sollte man auch zuerst nach den Wendepunkten suchen und falls es diese gibt, kann man noch überprüfen, ob die gefundenen Wendepunkte vielleicht auch Sattelpunkte sind.
Die Sattelpunkte haben die Eigenschaft, dass am Sattelpunkt für kurze Zeit die Steigung 0 herrscht - ansonsten ist alles genauso wie bei Wendepunkten. Die Bedingungen für einen Sattelpunkt sind also:
- f ' (x) = 0
- f '' (x) = 0
- f ''' (x)
0
Beispiel:
Verwendet wird als die selbe Funktion, die auch oben im Bild für den Sattelpunkt zu sehen ist.
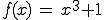
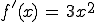
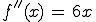
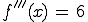
Jetzt wird erstmal nach Wendepunkten gesucht.
Für diese muss gelten f '' (x) gleich 0 und f ''' (x) ungleich 0.
Also nur die beiden letzten Bedingungen des Sattelpunktes.
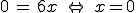
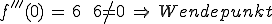
Ein Wendepunkt liegt also bei x=0.
Jetzt wird noch geprüft, ob dieser Wendepunkt vielleicht ein Sattelpunkt ist.
Dazu wird der x-Wert (also 0) in die 1. Ableitung eingesetzt (f ' (x)).
Ist das Ergebnis gleich Null, dann ist dieser Punkt ein Sattelpunkt, ansonsten nur ein ganz normaler Wendepunkt.
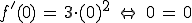
Die erste Ableitung ist also für diesen Wendepunkt 0.
Damit sind alle drei Bedingungen eines Sattelpunktes erfüllt - der Punkt ist ein Sattelpunkt.
Nun rechnet man noch schnell die zugehörige y-Koordinate zur x-Koordinate aus, damit man den Punkt genau im Koordinatensystem bestimmen kann:
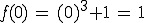
Der Sattelpunkt liegt also bei (0 | 1).
Jetzt wird erstmal nach Wendepunkten gesucht.
Für diese muss gelten f '' (x) gleich 0 und f ''' (x) ungleich 0.
Also nur die beiden letzten Bedingungen des Sattelpunktes.
Ein Wendepunkt liegt also bei x=0.
Jetzt wird noch geprüft, ob dieser Wendepunkt vielleicht ein Sattelpunkt ist.
Dazu wird der x-Wert (also 0) in die 1. Ableitung eingesetzt (f ' (x)).
Ist das Ergebnis gleich Null, dann ist dieser Punkt ein Sattelpunkt, ansonsten nur ein ganz normaler Wendepunkt.
Die erste Ableitung ist also für diesen Wendepunkt 0.
Damit sind alle drei Bedingungen eines Sattelpunktes erfüllt - der Punkt ist ein Sattelpunkt.
Nun rechnet man noch schnell die zugehörige y-Koordinate zur x-Koordinate aus, damit man den Punkt genau im Koordinatensystem bestimmen kann:
Der Sattelpunkt liegt also bei (0 | 1).
Kommentare (21)
Von neu nach altWir bitten um ihr Verständnis.
f'''(x) ungleich 0, wird da der x Wert aus f''(x) eingesetzt ?
Wenn die ersten drei Ableitung Null sind, kann es sich sehr wohl um einen Sattelpunkt handeln. Beispiel:
f(x)=x**5, f´(x)=5x**4, f´´(x)=20x**3, f´´´(x)=60x**2.
Die ersten drei Ableitungen sind Null und an der Stelle x=0 gibt es einen Sattelpunkt.
Die Sache ist die, dass bei f´´´(x)=0 lediglich keine Aussage über das Verhalten des Graphen der Funktion an der Wendestelle möglich ist. Ob Rechts-Links oder Links-Rechts lässt sich durch andere Methoden relativ einfach ermitteln.
Übrigens zeigt das Beispiel im vorigen Beitrag sehr schön, dass die zweite Ableitung an der Stelle eines Extremums Null sein kann. f´´(x)=0 liefert überhaupt keine Aussage über die Art des charakteristischen Punktes. Der Satz der Analysis lautet nämlich: Aus f´´(x)> 0 (<0) folgt, dass ein Minimum (Maximum) vorliegt. Und nicht umgekehrt. Es gibt somit keine Äquivalenz beider Aussagen. Letzteres wird in der Schulmathematik in schönster Regelmäßigkeit "vergessen" oder einfach nicht berücksichtigt.
das, was Wichtl schrieb ist nicht richtig. Die hinreichende Bedingung für Wendepunkte (also die zusätzliche Bedingung, bei der erst richtig bewiesen wird, dass es sich um einen Wendepunkt handelt), lautet: f'''(x) ungleich 0.
Wann ist das der Fall?
Betrachten wir zum Beispiel die Funktion f(x)=x^4
Die notwendige Bedingung f''(x)=0 würde für die Wendestelle x=0 ergeben. Wenn wir 0 in f'''(x) einsetzen erhalten wir null. Die notwendige Bedingung ist nicht erfüllt! Wir haben somit keinen Wendepunkt bei x=0. Bei Betrachtung des Graphen von x^4, handelt es sich bei x=0 um einen Extrempunkt, keinen Wendepunkt!
Um einen Sattelpunkt zu beweisen muss er folgende Bedingungen erfüllen:
* f '' (x) = 0 (notw. Bed.)
* f ''' (x) ungleich 0 (hinr. Bed.)
und zusätzlich muss die Steigung null sein an der Wendestelle.
==> zusätzlich muss gelten:
f'(x)=0 , mit x= errechnete (bereits bewiesene!)Wendestelle (bereits bewiesene!)
Ich hoffe ich konnte helfen kurz vorm Abi^^. bin auch dabei ;)
Beim vorherigen Kapitel (Wendepunkte) schrib wichtl:
"Wenn die 3. Ableitung = 0 ist, dann hat man einen Sattelpunkt."
Nun steht aber oben bei den Bedingungen, dass die 3. Ableitung ungleich 0 sein muss. Und so ist es ja hier auch gerechnet: 3. Ableitung ungleich 0 > WP ...und dann in 1. Ableitung einsetzen um herauszufinden, ob es ein SP ist. Aber was ist denn nun richtig?^^.... 3. Ableitung gleich oder ungleich 0?
Danke für alles =))))
Respekt)))
beste grüße,
Longdonganditheke