1. Einleitung
Polstellen sind diejenigen x-Werte, an denen eine Funktion kurzzeitig unterbrochen ist. Man nennt sie daher auch Definitionslücken. An Polstellen lässt sich also kein y-Wert für einen gewählten x-Wert finden, während die y-Werte in der direkten Umgebung des x-Wertes gegen unendlich streben.
Die Funktion
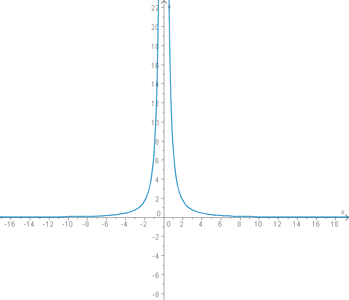
2. Beispiel 1
Die Funktion
hat eine Polstelle bei x=0. Wie man leicht erkennen kann, wird der Nenner Null sobald man für x Null einsetzt und damit ist die Funktion an dieser Stelle nicht definiert.
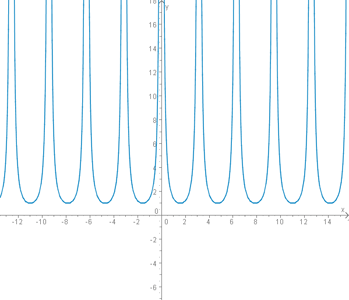
3. Beispiel 2
Die Funktion
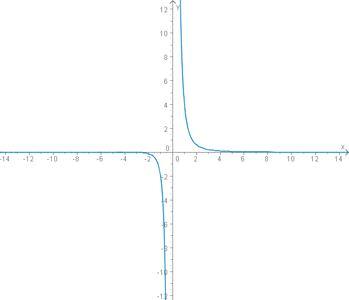
4. Beispiel 3
Die Funktion
hat eine Polstelle bei x=0. Wie leicht zu erkennen ist, haben die y-Werte direkt vor und direkt nach der Polstelle unterschiedliche Vorzeichen. Daher bezeichnet man Polstellen dieser Art auch als Polstellen mit Vorzeichenwechsel.