Polstellen (Thema: Analysis)

Wo ist eine Funktion nicht definiert?

1. Einleitung


Polstellen sind diejenigen x-Werte, an denen eine Funktion kurzzeitig unterbrochen ist. Man nennt sie daher auch Definitionslücken. An Polstellen lässt sich also kein y-Wert für einen gewählten x-Wert finden, während die y-Werte in der direkten Umgebung des x-Wertes gegen unendlich streben.

Die Funktion
f(x)=1/x^2
hat beispielsweise bei x=0 eine Polstelle (0 hoch 2 ist Null und ein Bruch ist nicht definiert falls er Null im Nenner hat).

2. Beispiel 1


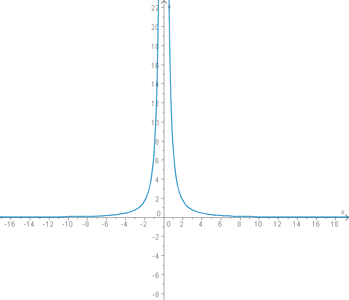
Die Funktion
f(x)=7/x^2


f(x)=7/x^2

hat eine Polstelle bei x=0. Wie man leicht erkennen kann, wird der Nenner Null sobald man für x Null einsetzt und damit ist die Funktion an dieser Stelle nicht definiert.



3. Beispiel 2


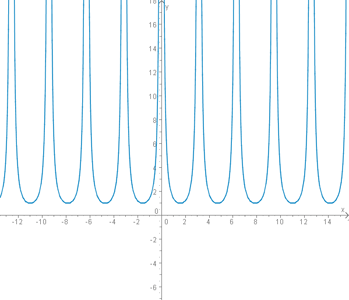
Die Funktion
f(x)=1/(sin(x))^2


f(x)=1/(sin(x))^2
hat Polstellen bei allen Vielfachen von pi. Oder mathematischer geschrieben:

P_a=a*pi, a Element aus Z



4. Beispiel 3


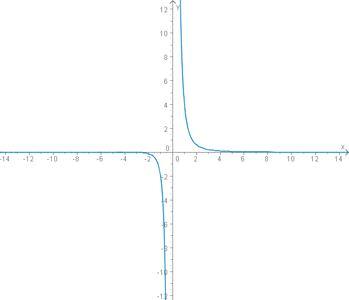
Die Funktion
f(x)=(1+x)/(x^3)

f(x)=(1+x)/(x^3)

hat eine Polstelle bei x=0. Wie leicht zu erkennen ist, haben die y-Werte direkt vor und direkt nach der Polstelle unterschiedliche Vorzeichen. Daher bezeichnet man Polstellen dieser Art auch als Polstellen mit Vorzeichenwechsel.

Kommentare (12)

Von neu nach alt
Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.
Asymptoten wäre noch ein Themengebiet oder ich hab es ausversehen überlesen
ArnoNuehm (Gast) #
einfach den nenner, also das was unter dem bruchstrich geschrieben steht, gleich 0 setzen. Das ergebnis liefert dir den wert, bei dem es sich um eine polstelle handelt.
ArnoNuehm (Gast) #
Gibt es denn hier keinen Rechenweg? Muss man erst den Graphen zeichnen und dann ablesen, bzw. ausprobieren wo diese Polstellen sind? Und was hat man davon, wenn man sie nun herausgefunden hat? Die anderen Artikel sind größtenteils gut und vom Umfang her ausreichend, aber nach dem hier weiß ich nicht viel mehr als zuvor.
Klara Kurzer (Gast) #
Das Prinzip mit dem Vorzeichenwechsel bereitet mir noch gewisse Probleme, kann mir jemand sagen, wie das im Allgemeinen definiert ist?
Shellshock (Gast) #
lustig
Ajaja (Gast) #
Ich hasse Mathe!
ArnoNuehm (Gast) #
Also Eimers Kommentar stimmt zwar, ist aber nicht sehr hilfreich, der Artikel ist auf jeden Fall unvollständig solang der von ArnoNuehm hervorgehobene Unterschied zwischen Nenner = 0 und Zähler&Nenner = 0 deutlich wird...
Irgendwer (Gast) #
Polstellen sind immer!!!! Definitionslücken, aber Definitionslücken sind oft auch hebbare Lücken, also nicht immer zwangsläufig Polstellen.

Wenn man Kommentare schreibt, sollte man sich vorher auch richtig informieren!!!
Eimer (Gast) #
Polstellen sind immer!!!! Definitionslücken, aber Definitionslücken sind oft auch hebbare Lücken.

Wenn man Kommentare schreibt, sollte man sich vorher auch richtig informieren!!!
Eimer (Gast) #
Stimmt! Bei einer gebrochenrationalen Funktion ist Polstelle nicht gleich Definitionslücke.

Polstelle ist dann an einer Stelle x, wenn für dieses x der Nenner 0 wird, der Zähler aber nicht.

Definitionslücke ist dann an einer Stelle x, wenn für dieses x der Nenner und acuh der Zähler 0 wird.



Bsp.: f(x)=(8x-2)/(x-2)

--> x=2 ist Polstelle (Nenner =0, Zähler ungleich 0)



Bsp.: f(x)=(x^2-2x)/(x-2)

--> x=2 ist Definitionslücke (Nenner & Zähler sind 0)
ArnoNuehm (Gast) #
Alle Kommentare zeigen (12)
Um unsere Webseite für Sie optimal zu gestalten und fortlaufend verbessern zu können, verwenden wir Cookies. Durch die weitere Nutzung der Webseite stimmen Sie der Verwendung von Cookies zu. Weitere Informationen zu Cookies erhalten Sie in unserer Datenschutzerklärung. OK