Eines der zentralsten aber auch einfachsten Themen der Differentialrechnung ist das Finden von Nullstellen. Nullstellen sind alle Punkte, an denen der Graph einer Funktion die x-Achse berührt oder schneidet.
Graph der Funktion f(x)=x^2-10 .
Nullstellen sind mit Pfeilen markiert.
Damit ein Graph die x-Achse berührt/schneidet, muss der y-Wert bei Null liegen. Daher auch der Name "Nullstellen".
In den meisten Fällen ist es also denkbar einfach, die Nullstellen zu errechnen: Man muss einfach die Funktion mit 0 gleichsetzen.
Beispiel:
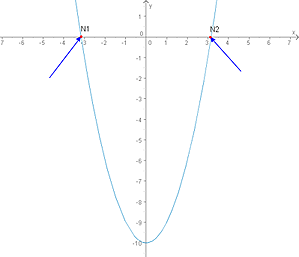
Damit sind die beiden Nullstellen (gerundet!) etwa N1 (-3|0) und N2 (3|0). Wie man oben im abgebildeten Graphen sehen kann, ist das auch richtig.
Wie bereits erwähnt, benötigt man bei der Berechnung der Nullstellen immer wieder die pq-Formel. Daher gibts die hier nochmal für alle, die sie bereits wieder vergessen haben:
Wiederholung
Die bisher dargestellte Vorgehensweise funktioniert recht einfach bei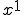
(also x) und 
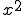. Sobald der Exponent aber größer wird, muss man in vielen Fällen die Polynomdivision anwenden.
Dabei muss man zunächst durch Probieren eine Nullstelle N finden. Danach teilt man die Funktion durch x + (-N). Dies führt man so lange fort, bis man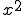 erhält - ab dann kann man mit der pq-Formel einfacher weitermachen.
Beispiel:
Einige Videos zum Thema mit Beispielen und weiteren Erklärungen:
Graph der Funktion f(x)=x^2-10 .
Nullstellen sind mit Pfeilen markiert.
Damit ein Graph die x-Achse berührt/schneidet, muss der y-Wert bei Null liegen. Daher auch der Name "Nullstellen".
In den meisten Fällen ist es also denkbar einfach, die Nullstellen zu errechnen: Man muss einfach die Funktion mit 0 gleichsetzen.
Beispiel:
Funktion: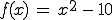 
Diese Funktion ist übrigens die gleiche, die auch oben im Bild zu sehen ist.
Mit 0 gleichsetzen:
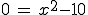
An dieser Stelle könnte man nun die PQ-Formel anwenden (muss man häufig bei der Berechnung von Nullstellen).
Es ist hier aber sichtlich einfacher, die 10 auf die andere Seite zu bringen und dann die Wurzel zu ziehen:
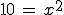
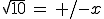
Diese Funktion ist übrigens die gleiche, die auch oben im Bild zu sehen ist.
Mit 0 gleichsetzen:
An dieser Stelle könnte man nun die PQ-Formel anwenden (muss man häufig bei der Berechnung von Nullstellen).
Es ist hier aber sichtlich einfacher, die 10 auf die andere Seite zu bringen und dann die Wurzel zu ziehen:
Damit sind die beiden Nullstellen (gerundet!) etwa N1 (-3|0) und N2 (3|0). Wie man oben im abgebildeten Graphen sehen kann, ist das auch richtig.
Wie bereits erwähnt, benötigt man bei der Berechnung der Nullstellen immer wieder die pq-Formel. Daher gibts die hier nochmal für alle, die sie bereits wieder vergessen haben:
Wiederholung
Auf eine gegebene Gleichung im Format
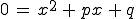
... wird die pq-Formel angewendet:
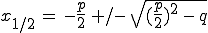
... wird die pq-Formel angewendet:
1. Nullstellenberechnung bei Polynomen
Die bisher dargestellte Vorgehensweise funktioniert recht einfach bei
Dabei muss man zunächst durch Probieren eine Nullstelle N finden. Danach teilt man die Funktion durch x + (-N). Dies führt man so lange fort, bis man
Beispiel:
Funktion: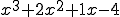 
erste Nullstelle (geraten): N1 = 1
Die Nullstelle N1 liegt also bei (1|0)
Nun wird durch x - 1 geteilt:
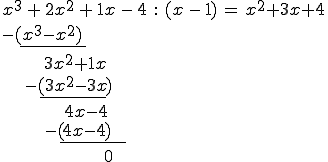
Die sich ergebende Funktion wird mit der pq-Formel bearbeitet:
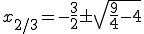
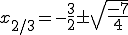
Unter der Wurzel steht eine negative Zahl, daher kann die Wurzel nicht aufgehen und dementsprechend können x2 und x3 auchkeine Werte annehmen. Die Funktion hat also nur eine Nullstelle: N1 (1|0)
erste Nullstelle (geraten): N1 = 1
Die Nullstelle N1 liegt also bei (1|0)
Nun wird durch x - 1 geteilt:
Die sich ergebende Funktion wird mit der pq-Formel bearbeitet:
Unter der Wurzel steht eine negative Zahl, daher kann die Wurzel nicht aufgehen und dementsprechend können x2 und x3 auchkeine Werte annehmen. Die Funktion hat also nur eine Nullstelle: N1 (1|0)
2. Links
Einige Videos zum Thema mit Beispielen und weiteren Erklärungen:
- Verschiedene Beispiele zur Nullstellenberechnung
- Nullstellen bei einer e-Funktion
- Nullstellenberechnung mit Hilfe des Zwischenwertsatzes.
Kommentare (20)
Von neu nach altWir bitten um ihr Verständnis.
Wenn du aber eine Biquadratischegleichung der Form (x^4+x^2+c) hast, wendest du ganz einfach die Substitution bzw. Ersetzungs- Technik an.
^= Hoch Zeichen
+/- z^(1/2) = x1; x2