Krümmung (Thema: Analysis)

links- oder rechtskrümmung?

1. Einleitung


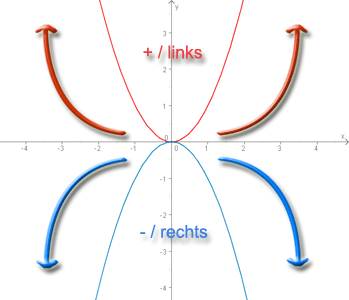
Die Angaben über das Krümmungsverhalten geben Aufschluss über den Verlauf des Graphen. Man unterscheidet zwei Fälle:

  • links gekrümmt
    auch genannt: positiv gekrümmt, konvex
  • rechts gekrümmt
    auch genannt: negativ gekrümmt, konkav

Bild zur Kruemmung
rot ist positiv gekrümmt/links gekrümmt/konvex,
blau ist negativ gekrümmt/rechts gekrümmt/konkav



2. Krümmungsverhalten nachweisen


Wie ein Graph an einer bestimmten Stelle gekrümmt ist, kann man über die zweite Ableitung herausfinden. Ist diese positiv, dann ist der Graph positiv gekrümmt/links gekrümmt/konvex (rot). Ist die zweite Ableitung negativ, dann ist der Graph negativ gekrümmt/rechts gekrümmt/konkav.



3. Beispiel


Der Graph der Funktion
f(x)=x^2
hat die 2. Ableitung
f''(x)=2
Wie man leicht sehen kann, kann man hier einsetzen was man will - es wird immer positiv bleiben und ist damit links gekrümmt/positiv gekrümmt/konvex an allen Stellen. Der Graph dieser Funktion ist auch oben im Bild zu sehen (roter Teil).

Kommentare (4)

Von neu nach alt
Das Erstellen neuer Kommentare ist aufgrund der Einführung der europäischen Datenschutz-Grundverordnung (DSGVO) derzeit deaktiviert.
Wir bitten um ihr Verständnis.
hay





ich denk es ist auch wichtig zu sagen das ein graph vllt die krümmungsrichtung wechselt und man dann wie bei der monotonie ein intervall angibt und die wendestellen als grenzen benutz .

mfg
schüler (Gast) #
Hallo an alle!



wichtig ist es nur zu wissen, wie die zweite Ableitung aussieht! f ist streng konvex <=> f''(x)> 0 auf X; f ist streng konkav <= f''(x) < 0 auf X. Man bedenke das aus der Krümmung nicht die Ableitung folgt! Beispiel f(x)=x^4



das zum Krümmungsverhalten



;-)
MatheStudent (Gast) #
Ich bin jezz nicht das Mathe-Ass, aber soweit ich weiß, bleibt der Term, egal was du einsetzt immer positiv bzw. ist dann Links-gekrümmt bzw. konvex. Ist dann halt nur etwas gestaucht bei hohen x-Werten.
Kuemmelor (Gast) #
Schön und gut, aber was ist mit Funktionen wie f(x)=36/(x^2+12) mit D=R
Pepe (Gast) #
Um unsere Webseite für Sie optimal zu gestalten und fortlaufend verbessern zu können, verwenden wir Cookies. Durch die weitere Nutzung der Webseite stimmen Sie der Verwendung von Cookies zu. Weitere Informationen zu Cookies erhalten Sie in unserer Datenschutzerklärung. OK