auch genannt: Definitionsmenge / Wertemenge
Der Definitionsbereich und der Wertebereich geben Aufschluss darüber, für welche x- und y-Werte eine Funktion definiert ist. Dabei gibt der "Definitionsbereich" die x-Werte an und der "Wertebereich" die y-Werte.
Die häufigste Form, den Definitionsbereich anzugeben ist
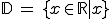
In diesem Fall gäbe es also für jeden x-Wert aus R einen y-Wert.
Entsprechend kann man den Wertebereich über
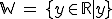
angeben.
Gesucht ist der Wertebereich und der Definitionsbereich zu
Wie leicht zu erkennen ist, geht die Funktion aus der x-Achse in beide Richtungen gegen unendlich. Man kann also jeden beliebigen x-Wert einsetzen und erhält einen y-Wert.
Dadurch aber, dass der eingesetzte x-Wert quadriert wird, kann der sich ergebende y-Wert aber niemals kleiner als Null werden. Die Funktion nimmt also nur y-Werte größer oder gleich 0 an.
Man kann also zusammenfassen:
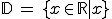
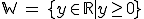
Gesucht ist der Wertebereich und der Definitionsbereich zu
Der Funktion kann man entnehmen, dass sich der ergebende Graph längerfristig wie eine Gerade verhalten muss, da sich x hoch 3 und x hoch 2 weitestgehend auflösen (zu x hoch 1). Das +17 macht bei ausreichend hohen x-Werten auch nicht mehr viel aus. Die Funktion kann auch ohne Probleme negative y-Werte bilden (durch das x hoch 3). Daher muss der Wertebereich alle Zahlen aus R enthalten. Nur für den Definitionsbereich gibt es eine Einschränkung: Er darf nicht Null enthalten, denn würde man Null einsetzen, dann würde auch der Nenner des Bruchs Null werden. Ein Bruch mit Null im Nenner ist aber nicht definiert.
Man kommt also zu folgendem Definitionsbereich/Wertebereich:
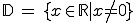
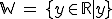
1. Einleitung
Der Definitionsbereich und der Wertebereich geben Aufschluss darüber, für welche x- und y-Werte eine Funktion definiert ist. Dabei gibt der "Definitionsbereich" die x-Werte an und der "Wertebereich" die y-Werte.
Die häufigste Form, den Definitionsbereich anzugeben ist
In diesem Fall gäbe es also für jeden x-Wert aus R einen y-Wert.
Entsprechend kann man den Wertebereich über
angeben.
2. Beispiel 1
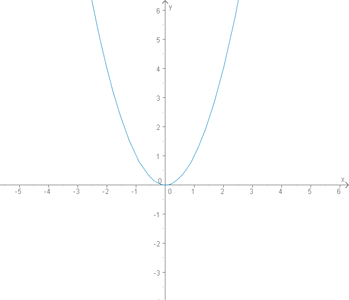
Gesucht ist der Wertebereich und der Definitionsbereich zu
Wie leicht zu erkennen ist, geht die Funktion aus der x-Achse in beide Richtungen gegen unendlich. Man kann also jeden beliebigen x-Wert einsetzen und erhält einen y-Wert.
Dadurch aber, dass der eingesetzte x-Wert quadriert wird, kann der sich ergebende y-Wert aber niemals kleiner als Null werden. Die Funktion nimmt also nur y-Werte größer oder gleich 0 an.
Man kann also zusammenfassen:
3. Beispiel 2
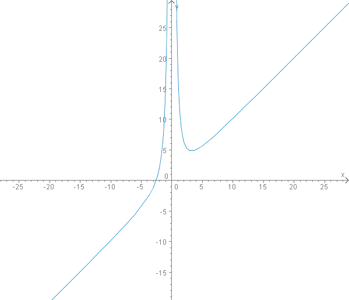
Gesucht ist der Wertebereich und der Definitionsbereich zu
Der Funktion kann man entnehmen, dass sich der ergebende Graph längerfristig wie eine Gerade verhalten muss, da sich x hoch 3 und x hoch 2 weitestgehend auflösen (zu x hoch 1). Das +17 macht bei ausreichend hohen x-Werten auch nicht mehr viel aus. Die Funktion kann auch ohne Probleme negative y-Werte bilden (durch das x hoch 3). Daher muss der Wertebereich alle Zahlen aus R enthalten. Nur für den Definitionsbereich gibt es eine Einschränkung: Er darf nicht Null enthalten, denn würde man Null einsetzen, dann würde auch der Nenner des Bruchs Null werden. Ein Bruch mit Null im Nenner ist aber nicht definiert.
Man kommt also zu folgendem Definitionsbereich/Wertebereich:
Kommentare (37)
Von neu nach altWir bitten um ihr Verständnis.
Ich danke Ihnen sehr!